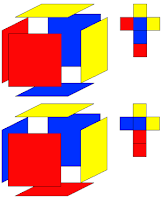
Enunciado
Me parece que poniendo este problema en el concurso nos hemos excedido. Para poder abordar la primera pregunta, es conveniente probar de cuántas formas se puede transformar un cuadrado en sí mismo, para ver el número de simetrías que hay que comprobar de una figura dada. La respuesta, incluyendo giros y simetrías, es el número 8. Junto a estas líneas podemos ver las ocho simetrías de un cuadrado con un dibujo en su interior, incluyendo el propio dibujo.
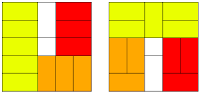
Representar todas las posibles formas de colocar las baldosas es un trabajo muy costoso. Por lo menos, a mí me ha supuesto bastante esfuerzo. Debemos numerar las diferentes formas en las que vamos situándolas, para asegurarnos recorrer todas las posibles y no duplicar esfuerzos, y a la vez eliminar aquellas que sean iguales, a través de una de las ocho simetrías del cuadrado, a otra creada previamente. Para detectar rápidamente repeticiones, he ideado marcar unas figuras representativas mediante colores, a las que he puesto nombres que me permitan recordarlas rápidamente. En el lateral vemos ahora ejemplos con esas figuras coloreadas. En el primero vemos una escalera larga amarilla y dos escaleras cortas. En la segunda, una mariposa en amarillo y dos escarabajos.
Sin más preámbulos, situamos el primer grupo de nueve formas distintas. Como es fácil apreciar, algunas baldosas están numeradas. Esta numeración representa el orden en que se han colocado las baldosas. Siempre tratamos de colocar la siguiente en una esquina superior izquierda, por tener una referencia (cuando hay varias, elegimos una). Contamos con dos posibles posiciones para esa baldosa: horizontal y vertical.
Primero colocamos la baldosa en horizontal. Cuando pasamos a la siguiente decoración, volvemos a la última de las baldosas situadas y la cambiamos a vertical (evidentemente, si ya está en vertical, esta baldosa ya se ha usado de todas las formas posibles, por lo que pasamos a mover la baldosa situada anteriormente). A la izquierda, vemos el segundo grupo de nueve formas.
En todos los diseños observamos baldosas sin numerar. Estas baldosas son las que se colocan de forma obligatoria porque las que hemos puesto anteriormente nos reducen el espacio. debemos borrarlas cuando construimos un nuevo diseño. Si hay espacio o no para colocar las baldosas de más de una forma, es algo bastante evidente. A la derecha vemos el tercer bloque de nueve formas diferentes.
Y por fin acabamos con los diseños de suelos. En total, si no me he equivocado, son 32 diseños distintos (sí que me he equivocado, mirar la actualización). Observa que los colores están puestos de manera algo arbitraria, para encontrar pronto las estructuras repetidas cuando vas generando las combinaciones. Primero busco las escaleras largas, y las pinto. Después, las escaleras cortas (el orden entre ellas es poco importante). Después, las mariposas (sólo hay en una de las estructuras), y, por último, los escarabajos. Así, aunque una determinada disposición podría tener escarabajos, si parte de sus baldosas forman parte de una escalera, no se colorea.
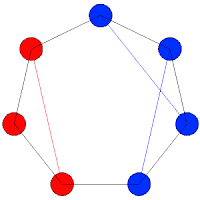
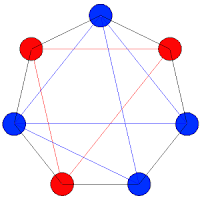
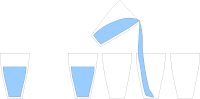
En cuanto a la segunda pregunta, si se puede o no cubrir con baldosas el segundo patio, la respuesta es que no. Podría intentarse hacer por tanteo, pero existe un sistema más corto que puede que sea muy eficaz en determinados problemas. Si observamos que la coloración inicial del patio parece un fragmento de ajedrez, nos daremos cuenta de que cada baldosa de las que vamos a colocar tapa un recuadro negro y uno blanco, siempre que esté sin partir. En el primer patio esto no es problema, pues hay la misma cantidad de cuadros negros y blancos, pero en el segundo patio no sucede lo mismo. al tapar la columna un recuadro de color blanco, hay dos recuadros más negros que blancos. Luego es evidente que no pueden cubrirse todas sin partir al menos una de las baldosas.
Actualización
Parece ser que hay un error en las últimas dos posibilidades. Por lo visto, estaba ya muy cansado cunado las comprobé. La número 32 es idéntica a la 30, haciendo una simetría de eje vertical. Y la 31 coincide mediante un giro de 180 grados con la 26 (tercer grupo de resultados). De forma que el número de posibilidades se reduce a 30.
Por cierto, la división de un espacio en celdas pequeñas (o tapar con baldosas) sin dividir la forma de estas celdas se llama teselar, y a la baldosa o celda, teselas. Hay muchos problemas en los que aparece este objetivo.