Un cuadrado en un triángulo
En los comentarios al enunciado se ha dado una solución basada en geometría analítica, es decir, en coordenadas de rectas.
Triángulo con cuadrado
También podemos solucionarlo mediante triángulos semejantes.
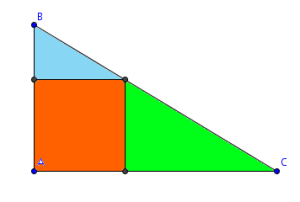
Como podemos comprobar comparando ángulos, dibujar el cuadrado dentro del triángulo deja dos triángulos disjuntos semejantes al original, cuyos lados, originalmente, medían 21, 28 y 35.
Si suponemos que la longitud del lado del cuadrado es x, el cateto menor de uno de los triángulos medirá x, y el mayor del otro también medirá x. De aquí, deducimos que el factor de escala que transforma el triángulo original en el pequeño es x/28, y el que transforma el original en el grande es x/21.
Por lo tanto, las hipotenusas medirán, respectivamente, 35*x/28 = 5*x/4 y 35*x/21 = 5*x/3. Y entre las dos, como se puede apreciar, suman la hipotenusa original, es decir, 5*x/4 + 5*x/3 = 35, de donde (15*x + 20*x)/12 = 35x/12 = 35, por lo que x mide 12.
Por lo tanto, el área del cuadrado mide 144 centímetros cuadrados, mientras que la del triángulo original era de 21*28/2 = 294, que es algo más del doble del cuadrado.
No hay comentarios:
Publicar un comentario