El menor perímetro

Enunciado

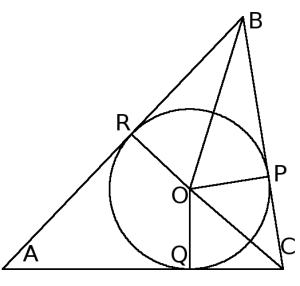
Si tratamos de dibujar varios triángulos que tengan la misma circunferencia inscrita, descubriremos que lo que tenemos que hacer es marcar tres puntos sobre la circunferencia y trazar las tangentes hasta que se corten. Es más, podemos fijar uno de los puntos y seguiremos obteniendo todos los triángulos posibles.

Un par de ejemplos

Como uno de los ángulos de la familia de triángulos que estamos estudiando es fijo, eso significa que dos de los puntos serán fijos, y además el tercer punto estará en el arco mayor comprendido entre ambos. En el dibujo he puesto dos de estos triángulos. A los vértices los he llamado A, B y C (A es el de ángulo fijo), y los puntos de tangencia, respectivamente opuestos a A, B y C, serán P, Q y R.

Es fácil ver que hay una parte del perímetro que está fija, la que va desde R hasta Q pasando por A, y el resto es la que puede variar. Además, como la distancia BP es la misma que BR, por simetría, y, de la misma forma, la distancia CP es la misma que CQ, en realidad sólo hay que tratar de que la distancia BC sea mínima (el perímetro total es la suma de RA, QA (fijas), RB, BP, QC, PC, y están repetidas dos veces).

Supongo que pronto habrás sospechado que el triángulo de menor perímetro es el isósceles, pero hemos de demostrarlo, y no es fácil.

Trazando lineas auxiliares

Si trazamos las líneas entre el centro de la circunferencia (al que llamamos O, como es tradición) y los vértices B y C vemos aparecer unos triángulos rectángulos muy interesantes, BPO y CPO. La longitud PO es un radio de la circunferencia, que es también fijo, llamémosle r, y por tanto tenemos que PB = r*cotg(B/2) y PC = r*cotg(C/2). De forma que BC = r*(cotg(B/2) + cotg(C/2)). Como r es constante, sólo hay que encontrar los valores de B y C para los que cotg(B/2) + cotg(C/2) es mínimo.

Además, hay una relación importante entre B y C, ya que A + B + C suman 180 grados, y A es fijo, por lo que B + C es una constante también. Esto puede sernos útil más adelante.

Tratemos de factorizar ahora cotg(B/2) + cotg(C/2) = cos(B/2)/sen(B/2) + cos(C/2)/sen(C/2) = (cos(B/2)*sen(C/2) + sen(B/2)cos(C/2))/(sen(B/2)sen(C/2)) = sen((B + C)/2)/(sen(B/2)sen(C/2)). Es evidente que sen((B + C)/2) es constante, por serlo B + C, por lo que ahora hay que encontrar el valor para el que sen(B/2)sen(C/2) se hace máximo.

Probablemente conoces las fórmulas que transforman un producto en una suma, y es el momento de aplicarlas, de manera que sen(B/2)sen(C/2) = (cos((B - C)/2) - cos((B + C)/2)/2. Está claro que, de nuevo, el segundo sumando (cos((B + C)/2)) es constante por serlo B + C, de forma que habrá que conseguir que cos((B - C)/2) sea lo mayor posible.

El valor de el ángulo (B - C)/2 está comprendido entre -90 y 90 grados, y en ese intervalo el valor del coseno máximo se alcanza cuando (B - C)/2 = 0, momento en el que B = C, por lo que el triángulo que buscábamos es isósceles.

Es posible que exista una demostración sin usar trigonometría, pero no creo que sea sencilla.