Policubos

Enunciado

Este es un problema bastante difícil, ya que incluye una parte de la formación matemática poco frecuente, que se llama visualización espacial.

3-Policubos numerados

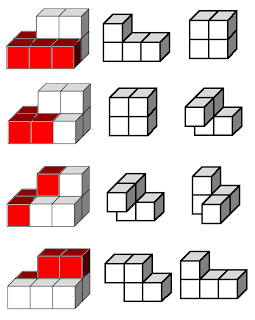
En primer lugar, es conveniente formar los policubos de orden cuatro a partir de los de orden 3, ya que son conocidos y es más fácil añadir un cubo que pegar 4 entre sí. Como es sencillo manipular los de orden 3, he puesto números distintos a los cuadrados "distintos" donde podemos añadir un nuevo cubo. Si es posible girar el policubo de forma que un cuadrado coincida con otro, el número es el mismo. Evidentemente, si el policubo tuviese caras "por detrás" distintas, habría tenido que hacer otras vistas, pero en este caso no ha sido necesario, pues al darle la vuelta coinciden con ellos mismos vistos de frente (son planos). Como vemos, el policubo más sencillo da lugar a tres de orden mayor, mientras que el otro da lugar a 7. Sin embargo, hay dos, como veremos, que coinciden.

Todos los 4-policubos

En este dibujo he puesto todos los policubos de orden cuatro que construimos de la forma que he indicado arriba. Los que llevan las letras A, B y C son creados a partir del policubo de orden 3 "recto", mientras que los que llevan las letras B, C, D, E, F, G y H son creados a partir del policubo de orden 3 "doblado". En total, son 8. Es particularmente difícil distinguir entre el E y el H, ya que uno es simétrico respecto al otro, pero no son iguales, si intentamos poner uno en la misma posición que el otro, uno de los cubos acaba apuntando hacia otro sentido (trata de imaginártelo).

Descomponer en dos policubos

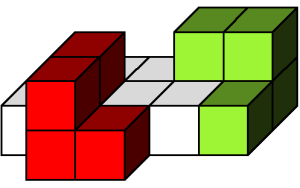
La segunda pregunta es más sencilla, y daba una pista fundamental por si te habías quedado sin dibujar algún policubo de los anteriores. Para descomponer la pieza, yo me he imaginado que partía de un cierto cubo e iba coloreando tres más "mentalmente", unidos al primero (observa que uno de los cubos no es visible en el dibujo, pero tú sí lo debes marcar como coloreado o no). Después, me fijaba si los otros cuatro que "sobraban" formaban o no una única pieza. Con este método he encontrado las cuatro descomposiciones posibles, que vemos en el dibujo que acompaña a este texto. La descomposición más sencilla es B + G, pero mucha gente encuentra también G + E. Como sólo piden dos, con esto estaría resuelto. Sin embargo, hay dos descomposiciones más, la D + B, que también es relativamente sencilla, y una muy extraña, que poca gente ve rápidamente, la E + H, que une a los dos 4-policubos más extraños.

La tercera pregunta era realmente difícil, ya que si te has dejado algún policubo sin dibujar es una pregunta muy sencilla, pero deja de serlo cuando tienes todos. Vamos a explicarlo. La figura a recubrir tiene 6 caras, las grandes tienen 8 caras de cubo visibles (cuadrados), las medianas, 4, y las pequeñas 2. En total, 28 cuadrados. Nuestros policubos pueden tapar, según dónde se pongan, entre 2 y 4 cuadrados cada uno.

Vayamos uno a uno probándolos. El A puede tapar 4 cuadrados, tanto en la cara mayor como en la mediana. El B y el C, pueden tapar 4 cuadrados de la cara mayor o 3 en la cara mediana. El D y el G, pueden tapar 4 cuadrados en la cara mayor, pero sólo 2 en las demás.

Colocando dos policubos

El policubo F puede tapar 3 cuadrados de la cara mayor, pero sólo 2 si se emplea en otro sitio. Por último, los policubos E y H pueden tapar 3 policubos de la cara mayor, pero también 3 si se les sitúa como se ve en el dibujo, tapando un cuadrado de la cara mayor y dos de otra cara.

Si sumamos todo estos números, en teoría podríamos cubrir 4 + 4 + 4 + 4 + 3 + 3 + 4 + 3 = 29, así que en principio parece que sí podríamos taparlo (por esto digo que si hemos olvidado alguno, la respuesta inmediata es que no, ya que obtenemos menos de 28 cuadrados tapados). Sin embargo, si tratamos de hacerlo veremos que fracasamos una vez tras otra ¿por qué?

Si revisamos la lista de cuadrados que podemos tapar, observamos que casi todos necesitan tapar cuadrados de la cara grande, así que a lo mejor por eso no hay suficientes. Podemos "perder" un cuadradito de todos los que podemos tapar, ya que el máximo que podemos tapar es 29 y tenemos que tapar 28, pero no más.

Vamos a fijarnos en cuántos de los 4-policubos necesitan ponerse en las caras grandes. El A no, puede ir en la lateral sin perder ningún cuadrado. El B y el C necesitan tapar 4 cuadrados de la cara grande para aprovecharse bien (aunque uno de los dos podría no estar del todo aprovechado). El D y el G, necesitan ir en la grande, tapando 4 cada uno. El F tiene que tapar 3 de la cara grande, y el E y el H necesitan tapar, para usarse bien, por lo menos uno de los cuadrados de la cara grande. En total, 21 cuadrados de las caras grandes, pero sólo hay 16 (8 + 8), de forma que no todos podrán ir ahí. aunque quitemos uno de los que cubre 4, y lo usemos tapando 3 en otra cara, seguiremos teniendo que tapar 21 - 4 = 17 cuadrados de las caras grandes, y sabemos que no se puede, pues sólo hay 16.

Por lo tanto, es imposible, aunque cuesta comprobarlo (desde luego, no se pueden probar todas las combinaciones posibles en un tiempo razonable). Probablemente, baste usar un único 4-policubo más para taparlo.