El incentro y la altura
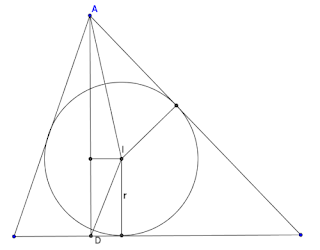
Este es uno de los problemas más complicados de geometría del triángulo que podemos encontrar en estos niveles. Hemos de observar que los elementos que salen en la fórmula deben relacionarse para comprobar la igualdad. Podemos empezar situando el segmento DI en un triángulo al que apliquemos el teorema del coseno, ya que está al cuadrado y no parece formar parte de ningún triángulo rectángulo que nos aporte nada.
Observamos entonces el triángulo ADI, del que obtenemos DI2 = ha2 + AI2 - 2 cos(DAI)*AI*ha. Lo que queremos lograr es que sea igual a (2R - ha)(ha - 2r) = 2R*ha - 4r*R - ha2 + 2r*ha. Aparentemente, no guardan mucha similitud, pero poco a poco iremos acercándonos.
El término 2 cos(DAI)*AI*ha admite una transformación, ya que cos(DAI)*AI es el segmento de la altura proyección ortogonal de AI, por lo que equivale a ha - r, ya que el radio que va desde I hasta el lado BC es paralelo a ha. Por tanto, la fórmula queda DI2 = ha2 + AI2 - 2*ha2 + 2r*ha = AI2 - ha2 + 2r*ha.
Observa que lo único que queda por probar es que AI2 = 2R*ha - 4r*R y el problema quedará probado.
Sin embargo este es el punto más complicado de toda la fórmula. Si observamos AI en el triángulo rectángulo que forma con el radio y uno de los dos lados adyacentes a A, tenemos que AI = r/sen (A/2). Descomponiendo el triángulo en tres triángulos de altura r desde I, se tiene que el área completa del triángulo, que podemos llamar S, es r*(a + b + c)/2, por lo que AI = 2*S/((a + b + c)*sen(A/2)).
Otra forma de calcular S es b*c*sen(A)/2 = b*c*sen(A/2)*cos(A/2), por lo que AI = 2*b*c*cos(a/2)/(a + b + c).
Una fórmula que hemos de aplicar aquí es una de las llamadas fórmulas de Briggs, que expresan las razones de los ángulos medios de un triángulo en función de los lados, según la cual, cos2(a/2) = (a + b + c)*(b + c - a)/(4*b*c). En este caso, obtenemos que AI2 = 4*b*b*c*c*(a + b + c)*(b + c - a)/(4*b*c*(a + b + c)2) = b*c*(b + c - a)/(a + b + c).
Tal vez lo más complicado de relacionar sea el radio de la circunferencia circunscrita (también llamado circunradio). Como se ve en el dibujo, si lo trazamos desde el circuncentro a los tres vértices, divide el triángulo en tres triángulos isósceles. Recuerda que estamos hablando de un triángulo acutángulo, ya que en caso contrario, el circuncentro no está en el interior. Cada uno de esos triángulos isósceles tiene dos lados de lado R y otro con el mismo tamaño que uno de los lados del triángulo. Debido a que los ángulos de los vértices de un triángulo están inscritos en la circunferencia, el ángulo que forman los radios es exactamente el doble que el ángulo opuesto al lado del triángulo. Si el lado, como en la figura, es a, el ángulo del triángulo isósceles será 2A. Y el triángulo isósceles se divide en dos triángulos rectángulos de hipotenusa R y ángulo A. Por eso R*sen(A) = a/2. También se suele escribir que S = b*c*a/(4R), derivado de que S se calcula como b*c*sen(a).
Claro que, como b*c*a/(4R) = a*ha/2, tenemos que b*c = 2R*ha. Nuestra fórmula queda AI2 = b*c*(b + c - a)/(a + b + c) = 2R*ha*(b + c - a)/(a + b + c).
Observa que ahora sólo nos queda probar que ha*(b + c - a)/(a + b + c) = ha - 2r.
Volviendo a calcular el área del triángulo de dos formas, tenemos que 2*S = a*ha = r*(a + b + c), de donde tenemos que a + b + c = aha/r y b + c - a = a + b + c - 2a = aha/r - 2a.
Por eso, ha*(b + c - a)/(a + b + c) = ha*(aha/r - 2a)/(aha/r) = ha*(aha - 2ar)/(aha) = ha*(ha - 2r)/(ha) = ha - 2r.
Recapitulando, ahora tenemos que en efecto AI2 = 2R*(ha - 2r) = 2R*ha - 4r*R y por tanto DI2 = AI2 - ha2 + 2r*ha = 2R*ha - 4r*R - ha2 + 2r*ha, que es la igualdad que debíamos probar.