Un cuadrilátero especial
En mi opinión, sobra el adjetivo de convexo, ya que si no lo fuese, una de sus dos diagonales sería externa al cuadrilátero y no podría bisecar el área.
Estudiemos las relaciones que se plantean en un cuadrilátero en el que una diagonal biseca el área.
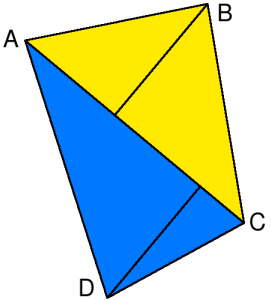
Una diagonal AC, como la que se ve en la figura, divide un cuadrilátero ABCD cualquiera en dos triángulos, ABC y ACD. Si ambos tienen la misma área, como propone el problema, tienen mucho en común, pues comparten un lado y el área.
Pensando en que cada uno de los triángulos cumplen la igualdad del área, es decir, su área es la mitad de la base por la altura, si tomamos como bases los lados comunes, llegamos a la conclusión de que tienen igual su altura sobre el lado común (AC en el dibujo).
Pensemos ahora en la otra diagonal, BD. Puesto que corta a la primera diagonal en un punto P, divide a cada triángulo de los que hemos visto en dos. Si observamos los dos triángulos que quedan a uno de los dos lados de la diagonal BD (por ejemplo, BCP y CDP), veremos que tienen un lado en común, CP, y la altura sobre ese lado igual (es igual a la de los triángulos originales, antes de trazar BD). Es decir, que tienen la misma área.
Ahora bien, si la segunda diagonal también biseca el área, los dos pares de triángulos de un lado tendrán la misma área que los dos del otro lado, y, puesto que son iguales en área entre sí, los cuatro triángulos en los que dividen las dos diagonales al cuadrilátero tienen la misma área.
Además, tienen todos ellos la misma altura sobre el segmento AC, como ya hemos visto, por lo que las bases que están apoyadas sobre este segmento, AP y CP son también iguales. Es decir, que P es exactamente el centro de AC.
Razonando de la misma forma con la otra diagonal, P también es el centro de BD, por lo que los triángulos opuestos (por ejemplo, APB y CPD) son iguales y por lo tanto los lados opuestos del cuadrilátero son paralelos, razonando por semejanza de triángulos (Teorema de Thales, por ejemplo).



No hay comentarios:
Publicar un comentario