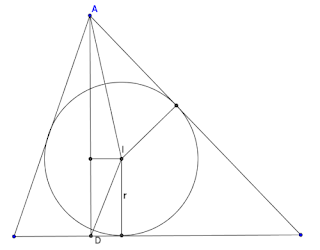
El incentro y la altura

Enunciado

El incentro y la altura

Este es uno de los problemas más complicados de geometría del triángulo que podemos encontrar en estos niveles. Hemos de observar que los elementos que salen en la fórmula deben relacionarse para comprobar la igualdad. Podemos empezar situando el segmento DI en un triángulo al que apliquemos el teorema del coseno, ya que está al cuadrado y no parece formar parte de ningún triángulo rectángulo que nos aporte nada.

Observamos entonces el triángulo ADI, del que obtenemos DI² = h_a² + AI² - 2 cos(DAI)*AI*h_a. Lo que queremos lograr es que sea igual a (2R - h_a)(h_a - 2r) = 2R*h_a - 4r*R - h_a² + 2r*h_a. Aparentemente, no guardan mucha similitud, pero poco a poco iremos acercándonos.

El término 2 cos(DAI)*AI*h_a admite una transformación, ya que cos(DAI)*AI es el segmento de la altura proyección ortogonal de AI, por lo que equivale a h_a - r, ya que el radio que va desde I hasta el lado BC es paralelo a h_a. Por tanto, la fórmula queda DI² = h_a² + AI² - 2*h_a² + 2r*h_a = AI² - h_a² + 2r*h_a.

Observa que lo único que queda por probar es que AI² = 2R*h_a - 4r*R y el problema quedará probado.

Sin embargo este es el punto más complicado de toda la fórmula. Si observamos AI en el triángulo rectángulo que forma con el radio y uno de los dos lados adyacentes a A, tenemos que AI = r/sen (A/2). Descomponiendo el triángulo en tres triángulos de altura r desde I, se tiene que el área completa del triángulo, que podemos llamar S, es r*(a + b + c)/2, por lo que AI = 2*S/((a + b + c)*sen(A/2)).

Otra forma de calcular S es b*c*sen(A)/2 = b*c*sen(A/2)*cos(A/2), por lo que AI = 2*b*c*cos(a/2)/(a + b + c).

Una fórmula que hemos de aplicar aquí es una de las llamadas fórmulas de Briggs, que expresan las razones de los ángulos medios de un triángulo en función de los lados, según la cual, cos²(a/2) = (a + b + c)*(b + c - a)/(4*b*c). En este caso, obtenemos que AI² = 4*b*b*c*c*(a + b + c)*(b + c - a)/(4*b*c*(a + b + c)²) = b*c*(b + c - a)/(a + b + c).

El circuncentro

Tal vez lo más complicado de relacionar sea el radio de la circunferencia circunscrita (también llamado circunradio). Como se ve en el dibujo, si lo trazamos desde el circuncentro a los tres vértices, divide el triángulo en tres triángulos isósceles. Recuerda que estamos hablando de un triángulo acutángulo, ya que en caso contrario, el circuncentro no está en el interior. Cada uno de esos triángulos isósceles tiene dos lados de lado R y otro con el mismo tamaño que uno de los lados del triángulo. Debido a que los ángulos de los vértices de un triángulo están inscritos en la circunferencia, el ángulo que forman los radios es exactamente el doble que el ángulo opuesto al lado del triángulo. Si el lado, como en la figura, es a, el ángulo del triángulo isósceles será 2A. Y el triángulo isósceles se divide en dos triángulos rectángulos de hipotenusa R y ángulo A. Por eso R*sen(A) = a/2. También se suele escribir que S = b*c*a/(4R), derivado de que S se calcula como b*c*sen(a).

Claro que, como b*c*a/(4R) = a*h_a/2, tenemos que b*c = 2R*h_a. Nuestra fórmula queda AI² = b*c*(b + c - a)/(a + b + c) = 2R*h_a*(b + c - a)/(a + b + c).

Observa que ahora sólo nos queda probar que h_a*(b + c - a)/(a + b + c) = h_a - 2r.

Volviendo a calcular el área del triángulo de dos formas, tenemos que 2*S = a*h_a = r*(a + b + c), de donde tenemos que a + b + c = ah_a/r y b + c - a = a + b + c - 2a = ah_a/r - 2a.

Por eso, h_a*(b + c - a)/(a + b + c) = h_a*(ah_a/r - 2a)/(ah_a/r) = h_a*(ah_a - 2ar)/(ah_a) = h_a*(h_a - 2r)/(h_a) = h_a - 2r.

Recapitulando, ahora tenemos que en efecto AI² = 2R*(h_a - 2r) = 2R*h_a - 4r*R y por tanto DI² = AI² - h_a² + 2r*h_a = 2R*h_a - 4r*R - h_a² + 2r*h_a, que es la igualdad que debíamos probar.

Lotería primitiva

Enunciado

Supuestamente, cada extracción de bolas es totalmente equiprobable con respecto a otra, como dice Lluís, de forma que lo único que podemos hacer para calcular la probabilidad de un suceso es calcular de cuántas formas podemos extraer una combinación premiada.

El premio gordo, es decir, que los seis números coincidan, basta ver cuántas extracciones diferentes hay. Podemos escoger la primera bola de 49 formas, la segunda de 48, la tercera de 47, y así sucesivamente, de forma que podríamos tener 49*48*47*46*45*44 extracciones diferentes. Una vez extraidas, las 6 bolas distintas, las ordenaríamos, para compararlas con otra extracción, y, puesto que pueden haber salido en cualquier orden, la primera puede acabar en cualquiera de las 6 posiciones, la segunda en 5, y así sucesivamente, es decir, pueden ordenarse de 6*5*4*3*2*1 formas diferentes. En definitiva, hay 49*48*47*46*45*44/6*5*4*3*2*1 = 13983816 extracciones diferentes. Eso quiere decir que la probabilidad de acertar la combinación es de 1/13983816.

Si buscamos que nuestra combinación coincida con cinco números y el otro no, hay 6 formas en las que podemos coincidir cinco de nuestros números con los de la combinación ganadora, y el otro no debe coincidir, por lo que debe ser uno de los 43 restantes. Eso quiere decir que la probabilidad será de 6*(6*5*4*3*2*43/(49*48*47*46*45*44)) = 43/2330636.

Si además queremos acertar el complementario, nuestro número no acertado debe coincidir con el que se extrae de los 43 que no han sido escogidos, por lo que la probabilidad será la anterior dividida por 43, es decir, 1/2330636.

Para calcular la probabilidad de acertar 4 (y fallar dos), la cosa se complica, puesto que debemos escoger los 4 que acertamos entre 6, o, lo que es lo mismo qué dos no acertamos de los 6, lo que podemos hacer de 6*5/2 = 15 formas diferentes. Eso quiere decir que la probabilidad será 15*(6*5*4*3*43*42)/(49*48*47*46*45*44) = 645/665896 = 0.00096862.

El último cálculo difícil se hace para la probabilidad de acertar 3 (y fallar otros 3). Es necesario calcular cuántos tríos podemos elegir entre las 6 bolas seleccionadas para acertarlos, y siguiendo la mecánica anterior, serán 6*5*4/(3*2) = 20 formas diferentes, lo que da lugar a una probabilidad de 20*(6*5*4*43*42*41)/(49*48*47*46*45*44) = 8815/499422 = 0.01765.

Colección de cubos

Enunciado

Es difícil dar una solución más precisa que la que ha dado Alex en los comentarios, aunque debo decir que hay que tener un poco más de cuidado leyendo el enunciado (y sumando).

En efecto, como se trata de pintar caras blancas o negras, los cubos son iguales si los puedes situar de la misma forma, y diferentes si es imposible.

Por lo tanto, si sólo pintas una única cara de color negro y las demás blancas, sólo hay un posible cubo.

Si pintas dos caras negras sólo tienes dos posibilidades, que las caras estén enfrentadas o que no lo estén (y entonces ambas comparten una arista).

Si pintas tres caras negras, entonces también tienes dos posibilidades, que dos de ellas estén enfrentadas o que no lo estén ninguna de las negras (y entonces compartan todas un vértice).

Evidentemente, si hay cuatro caras negras, hay dos blancas y razonamos de forma idéntica que sólo hay dos posibles cubos.

Y por último, con cinco caras negras sólo hay una blanca y por tanto una única posibilidad. En definitiva, 1 + 2 + 2 + 2 + 1 = 8 cubos diferentes (en el enunciado advierte que se han de utilizar los dos colores en todos los cubos).

Tarjetas en pilas

Enunciado

Este problema, de apariencia sencilla y que no esconde conceptos complicados, es uno de los más difíciles de este nivel que he encontrado últimamente.

Podemos experimentar mentalmente lo que dice el enunciado, probando al principio con pocas tarjetas, para conseguir objetivos parciales, hasta dar con la solución al problema completo.

Es evidente que no se pueden poner todas las cartas en un mismo montón, porque se incumple rápidamente la segunda regla, ya que 2 es suma de las dos cartas de valor 1.

Es fácil también concluir que no bastan dos pilas de tarjetas, aunque el razonamiento empieza a complicarse. En uno de los montones estará el 1, y por la primera regla, deberá estar la otra tarjeta que tiene un 1. En ese montón no estarán las tarjetas que tienen un 2, que estarán en el otro. Si sólo hay dos montones, las que tienen 4 deben estar en el montón del 1, porque 2 + 2 = 4, y por eso en ese montón no puede haber una tarjeta con el 3, porque 1 + 3 = 4. Luego las tarjetas del 3 están en el montón del 2. Pues bien, es imposible ahora colocar las tarjetas del 5, ya que en uno de los montones 1 + 4 = 5 y en el otro 2 + 3 = 5.

Podemos experimentar ahora la forma de situarlas en 4 montones, ya que situarlas en 3 parece ser complicado y tal vez sea imposible. Esta tarea es sencilla y hay muchas formas de hacerlo. Una de ellas podría ser situar en uno de los montones 1, 3, 5, 7, 9, 11, 13, en otro 2, 6, 10, en otro 4, 12 y en el último el 8. Está claro que es posible. Además, practicando llegamos a habituarnos a la dinámica de clasificar las tarjetas, y nos preparamos para la última parte: ¿encontraremos una manera de distribuirlas en tres pilas, o será imposible?

Vamos a ser sistemáticos. Anota todos los números en un papel, rodéalos con un círculo cuando estén situados, y marca de alguna forma (con un puntito encima, por ejemplo) cuando se les impida estar en un montón.

Empezamos por las primeras tarjetas, estarán en un montón que para nosotros será el primero. Esto evita que en el mismo montón estén las tarjetas 2.

El montón en el que estén las tarjetas 2 le llamaremos segundo montón, y en él no pueden estar las tarjetas 4.

Estas tarjetas, las 4, puede estar en el primer montón o en el tercero. Podemos empezar suponiendo que están en el primero. Eso evita que podamos poner en él al 3 (4 - 1), al 5 (4 + 1) y al 8 (4 + 4). Si no obtenemos ningún resultado poniéndolas aquí, podemos cambiar más adelante.

Las tarjetas con el 3 podemos ahora ponerlas en el segundo y en el tercer montón. Supongamos que las sitúo en el segundo (también podemos cambiar más adelante, si fuese preciso). Eso hace que sea imposible situar en él al 5 (2 + 3) y al 6 (3 + 3).

Está claro que el 5, en este caso, debe ir en el tercer montón, donde no podemos poner ahora al 10 (5 + 5).

El 6, por su parte, podría ir en el primer o en el tercer montón. Supongamos que la sitúo en el primer montón, impidiendo que pongamos en el primer montón el 7 (6 + 1), el 10 (6 + 4) y el 12 (6 + 6).

El 10 sólo puede ir en el segundo montón, de donde impedimos poner en él el 7 (10 - 3), el 8 (10 - 2), el 12 (10 + 2) y el 13 (10 + 3).

El 7 entonces está obligado al tercer montón, impidiendo situar en él el 12 (5 + 7). Si has marcado de alguna forma los números que tienen prohibido situarse en algún montón, te habrás dado cuenta de que el 12 no puede ahora ponerse en ningún montón. Luego habrá que cambiar alguna de nuestras decisiones anteriores, para ver si existe alguna manera de resolver el problema o descubrimos que es imposible.

Cambiemos la última decisión, situando ahora el 6 en el tercer montón. Te recuerdo lo que teníamos en ese momento. En el primer montón, estaba el 1 y el 4, y no podíamos situar el 8. En el segundo montón, teníamos el 2 y el 3. En el tercer montón, en este caso, tenemos el 5 y el 6, pero no podemos situar el 10, el 11 o el 12.

Ahora seguiremos situando el 10, del que sabemos que no puede ir al tercer montón. Lo situamos en el primero, pudiendo también cambiarlo más adelante. Esto impide situar en el primero al 9 (10 - 1), y al 11 (10 + 1).

El 11, por lo tanto, se puede colocar sólo en el segundo montón, cerrando el paso al 8 (11 - 3), al 9 (11 - 2) y al 13 (11 + 2).

De nuevo nos obliga a situar al 9 en el tercer montón, lo que no añade más situaciones imposibles, afortunadamente.

También está obligado el 8 a ir al tercer montón, impidiendo situar en él al 13 (8 + 5).

Entonces el 13 está obligado a ir al primer montón, causando que el 12 no pueda situarse en él.

Y de esta forma, el 12 debe ir al segundo montón. Sólo nos queda un par de tarjetas, con el 7, y pueden ir en cualquiera de los tres montones.

Tenemos entonces esta distribución en tres montones: 1, 4, 10, 13 el primero, 2, 3, 11, 12 y 7 el segundo y 5, 6, 9 y 8 en el tercero. Por lo tanto tres es el menor número de montones necesario para distribuir los 13 pares de tarjetas.

No sé si estas tres formas de distribuir las tarjetas serán las únicas ¿alguien se atreve a buscar otra distinta?

La diferencia es 2009

Enunciado

Puesto que se trata de pares de enteros, es una ecuación diofántica.

Como todas las ecuaciones de este tipo, lo que hemos de intentar es factorizarla y razonar sobre los diferentes factores que aparecen. En este caso, hay dos potencias restadas, que pueden tratarse como diferencia de cuadrados, así que x² - y⁴ = (x - y²)*(x + y²) = 2009. Puesto que tanto x como y son números enteros, los dos factores polinómicos, (x - y²) y (x + y²) son factores enteros. Basta descomponer 2009 en factores primos para estudiar todos los productos posibles, tanto positivos como negativos, y estudiar los casos para averiguar el valor de x e y.

Antes de pasar a valores concretos, supongamos que x - y² = a y x + y² = b, donde a es menor que b (recuerda que y² siempre es positivo). En ese caso, a + b = 2*x, y b - a = 2*y². De ahí, tendremos que x = (a + b)/2 e y² = (b - a)/2. Es evidente que (b - a)/2 deberá ser un cuadrado perfecto para que podamos calcular con éxito un valor entero para y.

Ahora, factoricemos 2009 = 7*7*41, así que lo podemos expresar sólo de seis formas 2009 = 1*2009 = 7*287 = 41*49 y sus opuestos. Las diferencias de estos números son 2009 - 1 = 2008, cuya mitad, 1004, no es un cuadrado perfecto, 287 - 7 = 280, cuya mitad es 140, que tampoco es un cuadrado perfecto, y 49 - 41 = 8, cuya mitad es 4. Este producto es el único que podemos aprovechar.

De 49*41 obtenemos un valor para x de (49 + 41)/2 = 45, y un valor para y de +2 y -2, y de (-49)*(-45) obtenemos un valor para x de -45, y un valor para y de +2 y -2.

En resumidas cuentas, los únicos pares posibles son (45, 2), (45, -2), (-45, 2) y (-45, -2).

Impuesto en la aduana

Enunciado

Como dice Lluís en los comentarios, hay que suponer que la dependencia del impuesto respecto a la cantidad de barriles es lineal, es decir, que el impuesto es un porcentaje del valor de los barriles. También hay que suponer que los barriles que transportan los comerciantes son idénticos en valor para facilitar el cálculo.

Así, tendríamos que el primero pagó, de 64 barriles, 5 barriles y 40 francos, mientras que el segundo pagó por 20 barriles 2 barriles y le devolvieron 40 francos.

Como no conocemos el valor en francos de cada barril, podemos llamar a esta variable B, y el porcentaje del impuesto por cada barril sería I. Así, 64*I = 5*B + 40 y 20*I = 2*B - 40. No deja de ser un sistema de ecuaciones con dos incógnitas. Si elegimos mi sistema favorito para resolverlas, reducción, multiplicaríamos la primera por 2, obteniendo 128*I = 10*B + 80, mientras que la segunda la multiplicamos por 5, de forma que 100*I = 10*B - 200. Restándolas ordenadamente, obtenemos que 28*I = 280, es decir, que el impuesto por barril es de 10 francos, y poniendo esto en cualquiera de las dos ecuaciones iniciales, por ejemplo en la segunda, obtenemos que 200 = 2*B - 40, es decir, que 2*B = 240, o lo que es lo mismo, el precio de un barril sería de 120 francos.

Un punto en un triángulo equilátero

Enunciado

En un principio, el problema se debe plantear uniendo ese punto con los tres vértices del triángulo equilátero, que queda así dividido en seis triángulos rectángulos, distintos entre sí probablemente.

Si tratamos de resolverlo con un sistema de ecuaciones, probablemente obtendríamos una solución, aunque de manera lenta y costosa. Puede solucionarse el problema de una forma mucho más eficaz si observamos que su área se puede poner en función del lado de dos formas distintas, y calculamos el lado desde esas expresiones.

Por un lado, un triángulo equilátero de lado 1 se puede dividir en dos triángulos rectángulos, cuya hipotenusa mide el doble que uno de los catetos. Es evidente, por Pitágoras, que el otro cateto, que es la altura del triángulo equilátero, medirá √(1-1/4) = √3/2. Eso quiere decir que el área del triángulo equilátero de lado 1 es √3/4. Si el lado mide otra cantidad, x, el triángulo mantendrá una proporción de escala x, y su área mantendrá una escala de factor el cuadrado de x. Por tanto, se podrá calcular multiplicando el lado al cuadrado por √3/4.

En el caso en particular que nos ocupa, podemos unir los triángulos rectángulos que tienen un cateto común, formando tres triángulos cuyas bases son los lados del triángulo equilátero, sus alturas son 1, 2 y 3, y cubren todo el triángulo equilátero, es decir, que el área total se puede calcular sumando x*1/2 + x*2/2 + x*3/2 = x*6/2 = x*3.

Si esos dos valores producen el mismo resultado, es porque x*√3/4 vale lo mismo que 3, es decir, que x es 3 dividido entre √3/4. Puedes calcularlo de forma aproximada, o de forma exacta, y obtendrás que x vale 4√3, aproximadamente 6,9282.

Si lo intentas hacer con ecuaciones, es posible que te veas ante un sistema de 10 ecuaciones con 10 incógnitas, y varias de ellas de segundo grado. No parece una buena alternativa.

Sin embargo, entre los comentarios del enunciado, aparece una solución muy interesante que usa trigonometría, aunque los estudiantes de este nivel aún no la suelen dominar.

Tres números primos

Enunciado

De nuevo se trata de un problema en el que debemos seguir un tanteo inteligente para que no lleve demasiado tiempo.

En los comentarios podemos observar el método que propone Alex, que es bastante corto. Yo voy a proponer otro, pero no es mejor que el de Alex.

En primer lugar, observamos que son tres números que suman un número par, es decir que uno de ellos es par (o son los tres), pero eso quiere decir que uno de ellos es 2, que es el único primo que es par.

Si 2 es p, entonces q² + r³ = 198. Como r debe ser 3 o 5 (7³ = 343 es demasiado grande), probemos si hay algún q válido. Descubrimos que q² = 171 y eso es imposible, pues no es un cuadrado perfecto, o bien q² = 73, que tampoco es posible.

Si 2 es q, entonces, p + r³ = 196, y de nuevo r puede ser 3, pero en ese caso p = 169, y ese número no es primo (169 = 13*13), o r puede ser 5, en cuyo caso tenemos el primer resultado, 71 + 2² + 5³ = 200.

Si 2 es r, entonces tendremos que p + q² = 192. Aquí probaremos diferentes valores para q, lo que nos llevará algún tiempo.

Si q es 3, p vale 189 = 3*63, no es primo.

Si q es 5, obtenemos otro resultado, 167 + 5² + 2³ = 200.

Si q es 7, p vale 143 = 11*13, no es primo.

Si q es 11, obtenemos el resultado 71 + 11² + 2³ = 200.

si q es 13, obtenemos el resultado 23 + 13² + 2³ = 200.

Y q no puede ser 17 o mayor, puesto que 17² = 289 ya es mayor que el número que buscamos.

Así, tenemos estos cuatro posibles valores.