Enunciado
He de reconocer que esta configuración no la conocía. Puedes dar con ella de casualidad o trabajar de forma más sistemática.
Si tratamos de construir un grupo de posiciones con tres puntos que cumplan esta condición, cualquier trío en el que haya dos puntos a una unidad vale, independientemente de la posición que ocupe el tercero.
Con cuatro puntos, disponemos de dos posibilidades: o bien tenemos dos pares a distancia 1, o bien tres de ellos forman un triángulo equilátero de lado 1. Las demás distancias no importan, de nuevo.
Con cinco puntos, de nuevo tenemos dos posibilidades. Una de ellas consiste en un triángulo equilátero de lado uno y dos puntos a una distancia de una unidad entre ellos, y la otra en un pentágono cuyos lados miden todos uno (no necesariamente regular, los ángulos no importan). Es fácil extender estas dos posibilidades a partir de la anterior.
Con seis puntos, de nuevo tenemos la posibilidad de crear dos configuraciones. Una consiste en dos triángulos equiláteros de lado uno. La otra, en un triángulo equilátero de lado uno que comparte un lado con el pentágono de lados 1 del caso anterior, bien sea el tercer vértice interior o exterior al pentágono.
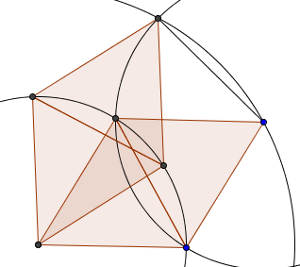
Configuración de siete puntos
Y de ahí, pasamos a construir la figura para siete puntos. Partamos de un caso de seis puntos o del otro, llegamos a la misma construcción, por lo que la posición es única. Podemos verla como un pentágono de lado uno, no regular, dentro del cual hay dos puntos de forma que uno de ellos está a una unidad de distancia de tres de los puntos, y el otro también, a una unidad de uno de los tres puntos del otro y de los otros dos. O bien como dos triángulos equiláteros de lado uno convenientemente situados para que dos de sus vértices estén a distancia uno, y los otros cuatro estén a distancia uno de un séptimo punto. Esta única configuración es la que buscamos.
Situemos el primer átomo en (0,0). (A)
El segundo en (1,0) (a una unidad del primero).(B)
El tercero, estará a una unidad de A y B, en (1/2, √(3)/2). (C)
El cuarto, a una unidad de B y C , en (3/2, √(3)/2). (D)
El quinto, a una distancia de √3 de A y de 1 de D, en ((15-√(33))/12, (5*√(3)+3*√(11))/12) (E)
El sexto, uno de los dos puntos a una unidad de distancia de A y de E, (5/6, √(11)/6) (F)
El séptimo, el otro de los puntos a una unidad de distancia de A y de E, ((5-√(33))/12, (53⁽1/2)+√(11))/12) (G)
Se da la circunstancia de que, por construcción, la distancia de F a G también es de 1.
Por lo tanto, valen uno las distancias: AB, AC, BC, BD, CD, DE, AF, EF, AG, EG, FG (11 distancias de las 21)
Por lo tanto para cada terna hay dos puntos a una unidad:
ABC
ABD
ABE
ABF
ABG todas AB
ACD
ACE
ACF
ACG todas AC
ADE DE
ADF AF
ADG AG
AEF AF
AEG AG
AFG AF
BCD
BCE
BCF
BCG todas BC
BDE
BDF
BDG todas BD
BEF EF
BEG EG
BFG FG
CDE
CDF
CDG todas CD
CEF EF
CEG EG
CFG FG
DEF EF
DEG EG
DFG
EFG todas FG