Pirámide numérica

Enunciado

Pirámide numérica

El primer número que podemos situar es el central de la tercera fila, que debe ser el 11 para que la diferencia sea 9.

Para el número restante de esa fila, que debe tener una diferencia de 4 con el 11, no podemos usar el 15, pues el propio 15 no puede ser la diferencia de dos números del 1 al 15. Por lo tanto, deberemos poner el 7.

Ahora, nos quedan sin usar los números 1, 3, 8, 10, 12, 13, 14 y 15. Ninguna de las diferencias que pueden proporcionar 7, 11 o 2 es única, pero si queremos usar el 6 para conseguir otro de la lista, es decir, llenar la casilla inmediatamente superior al 6 y la que está al lado, no queda más remedio que usar el 8 y el 14. Así, el 8 será el primer número de la cuarta fila y el 14, el segundo de la quinta.

Ahora, junto al 8 de nuevo no podemos usar el 15, por lo que no tendremos más remedio que usar el 1.

Evidentemente, junto al 1 habrá que situar el 12.

Ahora, junto al 12, como ya está usado el 14, hemos de situar el 10.

Para las últimas tres casillas sólo quedan por situar los números 3, 13 y 15. Puesto que los dos números finales de la quinta fila son 3 y 13, que son los únicos que se diferencian en 10, el que va en el centro es claramente el 15, y la única forma de cuadrar las restas es poner junto a ese número el 3 y el 13 en ese orden.

Una molécula de siete átomos

Enunciado

He de reconocer que esta configuración no la conocía. Puedes dar con ella de casualidad o trabajar de forma más sistemática.

Si tratamos de construir un grupo de posiciones con tres puntos que cumplan esta condición, cualquier trío en el que haya dos puntos a una unidad vale, independientemente de la posición que ocupe el tercero.

Con cuatro puntos, disponemos de dos posibilidades: o bien tenemos dos pares a distancia 1, o bien tres de ellos forman un triángulo equilátero de lado 1. Las demás distancias no importan, de nuevo.

Con cinco puntos, de nuevo tenemos dos posibilidades. Una de ellas consiste en un triángulo equilátero de lado uno y dos puntos a una distancia de una unidad entre ellos, y la otra en un pentágono cuyos lados miden todos uno (no necesariamente regular, los ángulos no importan). Es fácil extender estas dos posibilidades a partir de la anterior.

Con seis puntos, de nuevo tenemos la posibilidad de crear dos configuraciones. Una consiste en dos triángulos equiláteros de lado uno. La otra, en un triángulo equilátero de lado uno que comparte un lado con el pentágono de lados 1 del caso anterior, bien sea el tercer vértice interior o exterior al pentágono.

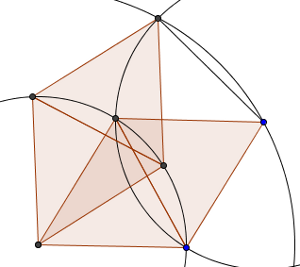
Configuración de siete puntos

Y de ahí, pasamos a construir la figura para siete puntos. Partamos de un caso de seis puntos o del otro, llegamos a la misma construcción, por lo que la posición es única. Podemos verla como un pentágono de lado uno, no regular, dentro del cual hay dos puntos de forma que uno de ellos está a una unidad de distancia de tres de los puntos, y el otro también, a una unidad de uno de los tres puntos del otro y de los otros dos. O bien como dos triángulos equiláteros de lado uno convenientemente situados para que dos de sus vértices estén a distancia uno, y los otros cuatro estén a distancia uno de un séptimo punto. Esta única configuración es la que buscamos.

Situemos el primer átomo en (0,0). (A)

El segundo en (1,0) (a una unidad del primero).(B)

El tercero, estará a una unidad de A y B, en (1/2, √(3)/2). (C)

El cuarto, a una unidad de B y C , en (3/2, √(3)/2). (D)

El quinto, a una distancia de √3 de A y de 1 de D, en ((15-√(33))/12, (5*√(3)+3*√(11))/12) (E)

El sexto, uno de los dos puntos a una unidad de distancia de A y de E, (5/6, √(11)/6) (F)

El séptimo, el otro de los puntos a una unidad de distancia de A y de E, ((5-√(33))/12, (53⁽1/2)+√(11))/12) (G)

Se da la circunstancia de que, por construcción, la distancia de F a G también es de 1.

Por lo tanto, valen uno las distancias: AB, AC, BC, BD, CD, DE, AF, EF, AG, EG, FG (11 distancias de las 21)

Por lo tanto para cada terna hay dos puntos a una unidad:

ABC

ABD

ABE

ABF

ABG todas AB

ACD

ACE

ACF

ACG todas AC

ADE DE

ADF AF

ADG AG

AEF AF

AEG AG

AFG AF

BCD

BCE

BCF

BCG todas BC

BDE

BDF

BDG todas BD

BEF EF

BEG EG

BFG FG

CDE

CDF

CDG todas CD

CEF EF

CEG EG

CFG FG

DEF EF

DEG EG

DFG

EFG todas FG

Sistema de ecuaciones

Enunciado

Está claro que es más fácil trabajar con variables normales que con potencias, de forma que vamos a transformar 2^x en a, 2^y en b y 2^z en c. Puesto que la función 2^x es creciente y positiva, los números a, b y c son positivos y la transformación es absolutamente reversible (cualquier resultado (a, b, c) válido está asociado a un único (x, y z)).

Las ecuaciones, así, se transforman en 3b - 1 = a + 1/a, 3c - 1 = b + 1/b, 3a - 1 = c + 1/c. Dada la simetría de la situación, vamos a estudiar lo que pasaría si las tres fuesen iguales, ya que en ese caso, 3a = 1 + a + 1/a, de donde 2a = 1 + 1/a, es decir 2a² - a - 1 = 0, que es una ecuación de segundo grado que tiene por soluciones 1 y -1/2. La solución negativa, evidentemente, no vale en este caso, y la solución positiva nos lleva a que (x, y, z) = (0, 0, 0).

Si los tres números no fuesen iguales, tendríamos un orden entre ellos. Tratemos de llegar a una contradicción. Estudiemos la función que transforma a cada uno de ellos en el otro. Despejando, tenemos que b = (a² + a + 1)/3a, c = (b² + b + 1)/3b y a = (c² + c + 1)/3c. Está claro que hay que estudiar la función y = (x² + x + 1)/3x.

Si estás acostumbrado a representar funciones, rápidamente detectarás que f(x) es mayor que 1 para todo los x positivos, y además, es creciente para valores por mayores que 1. Todo esto se puede estudiar de manera muy cómoda con la derivada, pero también de forma directa, ya que la solución válida anterior nos indica con qué número comparar.

Por lo tanto, a, b y c no sólo son mayores que 0, si no que deben ser mayores que uno. Y, puesto que a = f(c), c = f(b) y b= f(a), si uno de ellos es mayor que el otro rápidamente llegamos a una contradicción, puesto que si p > q, f(p) > f(q). Es decir, que los tres deben ser iguales y la única solución válida es (x, y, z) = (0, 0, 0).

Una cuestión de unos y ceros

Enunciado

Este problema ha tenido una solución oficial tan sencilla que no puedo evitar contarla: la idea es que al dividir un número entre otro, el resto es un número menor que el segundo, así que si dividimos los números de la sucesión 1, 11, 111, etcétera entre un número fijo, puesto que es una sucesión ilimitada, habrá dos que tengan el mismo resto. Y, por supuesto, la diferencia entre esos dos términos, que estará compuesta exclusivamente por unos y ceros, dará resto cero al dividirlo entre ese número fijo. Así, cualquier número tiene un múltiplo de esa forma.

Considero que esta solución requiere tener la afortunada idea de aplicar este principio, no es una técnica habitual.

Yo había usado, con algo más de trabajo, la expresión decimal de 1/(9N), ya que una expresión fraccionaria de esta expresión decimal, periódica, podía tener un denominador compuesto de nueves y ceros, y era sencillo ver que necesariamente era un múltiplo de 9N. Dividiendo por 9 a ambos lados, obtendríamos la igualdad deseada.

Por otra parte, el resultado se puede generalizar, ya que todo número tiene un múltiplo formado por la suma finita de una serie de potencias consecutivas de una base prefijada. ¿Alguien se anima?

Calculemos áreas

Enunciado

La clave de la primera figura es descomponer los hexágonos en seis triángulos equiláteros, llevando al hexágono grande a estar compuesto de los mismos triángulos.

En particular, los tres hexágonos pequeños tendrán un total de 18 triángulos pequeños, mientras que el diámetro del hexágono grande contendrá un total de cinco bases de triángulo de ese mismo tamaño.

En definitiva, puesto que el lado del triángulo también vale 3, al igual que el del hexágono, el lado del hexágono grande medirá 7,5 (observa que su radio coincide con el lado, y que es dos veces y media la longitud de un lado de triángulo).

El área de un triángulo equilátero, usando Pitágoras para calcular la altura, sabrás que es √3*x²/4, siendo x su lado, por lo que el área del hexágono será 3√3*x²/2, y la de los tres hexágonos, en nuestro caso, 81√3/2. Sin embargo, el hexágono grande tendrá un área de 675√3/8, por lo que el área sombreada medirá la diferencia, 351√3/8, aproximadamente 75,9937 centímetros cuadrados.

En el segundo dibujo, el del cuadrado, se reduce el problema a calcular el lado del cuadrado mayor (el del menor es claramente 3). Descomponiendo de nuevo los hexágonos en triángulos equiláteros, el lado del triángulo mayor será tres más cuatro veces la altura de uno de esos triángulos, es decir, 3√3/2. En total, el lado de este cuadrado será 3 + 6√3, por lo que el área del cuadrado medirá (3 + 6√3)². Y el área de los cuatro hexágonos será 54√3. En total, el área coloreada valdrá la diferencia, (3 + 6√3)² - 54√3, que aproximadamente vale 85,8231 centímetros cuadrados, si no me he equivocado.

La superficie del jardín

Enunciado

Es sencillo ver que la parte coloreada, respecto a uno de los cuatro cuadraditos en los que está dividido el jardín, representa un cuarto del área del cuadradito, ya que es un triángulo que tiene la altura total del cuadrado, y de base la mitad del lado, por lo que su área es una cuarta parte.

De esta forma, sabemos que el área del jardín completo será 16 veces mayor que la parte coloreada, es decir, 80 metros cuadrados.

El triángulo donde irán los rosales se puede dividir de forma sencilla en 6 triángulos de la misma área que el que tenemos, aunque evidentemente no todos de la misma forma. Eso supone que el área que ocuparán al final los rosales es de 30 metros cuadrados, es decir, que han plantado ya una sexta parte de ese área.

Partículas en colisión

Enunciado

Ya había visto un problema similar a este, con camaleones que cambian de color al encontrarse.

Lo primero que hay que observar es que las diferencias entre las cantidades que hay de cada par de partículas varía exclusivamente de 3 en 3. Es decir, si tenemos cantidades a, b y c de cada tipo de partículas, después de una colisión de las primeras con las segundas (y primeras y segundas pueden ser cualquiera), habrá a - 1, b - 1 y c + 2, con lo cual las diferencias entre primeras y segundas será igual, entre primeras y terceras habrá aumentado en tres (c + 2 - (a - 1) = c - a + 3). Lo mismo sucederá con las diferencias entre segundas y terceras.

En el estado inicial, las diferencias entre dos tipos de partículas son 20 = 30 - 10, 13 = 30 - 17 y 7 = 17 - 10. Ninguno de ellos es múltiplo de 3, por lo que nunca podrá llegar a ser cero, y en consecuencia no podrá haber un único grupo de partículas, ya que los otros dos no podrían nunca ser iguales.

Curiosamente, este método da una idea de cómo lograr que haya un grupo de partículas casi único, salvo una, quiero decir. Por ejemplo, podemos conseguir que todas menos una sean positivas, es suficiente hacer chocar dos veces positiva y neutra, hasta obtener 28 positivas, 14 negativas y 15 neutras. A partir de ahí, colisionamos 14 negativas y 14 neutras, logrando 56 positivas y una única neutra. De forma similar podríamos lograr todas menos una negativas (con una positiva) y todas menos una neutras (con una negativa, también).