Rodeado de circunferencias

Enunciado

Tres círculos con radios

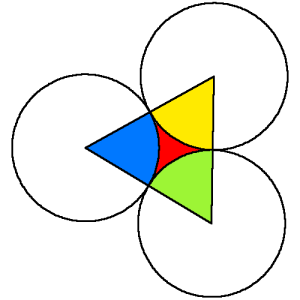
Como siempre en los problemas de geometría, hay que trazar algunas líneas que nos aportan mucha información. En este caso (como casi siempre) se trata de radios, que van desde los centros de las circunferencias, hasta los puntos de tangencia. Como los radios son perpendiculares a las tangentes, pertenecen cada dos de ellos a las dos semirrectas de la misma recta, es decir, que entre los 6 radios forman un triángulo, que además es equilátero, de lado 10 cm (el diámetro es 10, luego el radio es 5).

Además, si pintamos de diferentes colores las zonas que componen este triángulo, podemos apreciar que la parte que no está entre las tres circunferencias (la que está dentro de las circunferencias), forma tres arcos de circunferencia, cada uno de ellos de 60 grados, es decir, que es el arco del uno de los vértices de un triángulo. El área de los tres, si se sumara, sería 60 + 60 + 60 = 180, media circunferencia. Es decir que el área que buscamos es el área del triángulo menos el arco de media circunferencia de radio 5.

El área de un triángulo equilátero se calcula dividiéndolo en dos rectángulos mediante una altura, y aplicando el Teorema de Pitágoras. Así, la altura al cuadrado más medio lado al cuadrado es el lado completo al cuadrado, es decir, que la altura es la raíz cuadrada de la raíz de 3 multiplicada por la mitad del lado, en nuestro caso 5√3. El área, entonces, será 10*5√3/2 = 25√3.

El área de medio círculo será 25*π/2, de donde el área de la zona que se nos pide es 25√3 - 25*π/2 ≅ 4,0313.