Cubos de colores

Enunciado

Este problema pertenece a la misma familia de problemas que el de pintar triángulos del primer ciclo. Y el sistema para abordarlo es similar, tratar de citar uno a uno los casos (o las familias de casos) de forma que quede claro que no hay elementos repetidos entre los citados en un grupo y los citados en otro.

Posiciones iniciales

Supongamos que el cubo lo pintamos usando los colores amarillo, rojo y azul. Fijémonos sólo en las caras amarillas. Básicamente pueden tener dos posiciones distintas: o una es opuesta de la otra o está junto a ella (es adyacente). Vamos a analizar estos dos casos detenidamente. Para ilustrar este problema podemos optar por desplegar el cubo, separar un poco las caras (o romperlas) para que se vean las de detrás, o bien simular un giro que nos permita ver varias vistas del cubo para averiguar cómo está pintado por el lado que no podemos ver.

Amarillos opuestos

Amarillos opuestos

Ponemos las caras amarillas arriba y abajo. Las caras rojas, que están en las caras laterales, pueden ser opuestas o adyacentes, y está claro que eso da lugar a sólo dos casos distintos. Evidentemente, las caras azules son las que faltan por rellenar.

Amarillos adyacentes

Amarillos adyacentes,
otros opuestos

Ponemos una cara amarilla arriba y la otra en el lateral. Es fácil entender que podemos girar el cubo de forma que intercambiemos las dos caras, de forma que habrá que tener cuidado con ese cambio por si hiciese iguales dos decoraciones distintas. Si queremos poner las caras rojas opuestas, sólo podemos hacerlo de forma que estén ambas en el lateral, a ambos lados de la cara amarilla, y así las dos azules quedarán opuestas a las dos amarillas. También podemos hacer lo mismo con los colores cambiados, es decir, los azules opuestos entre sí y los rojos opuestos a los amarillos. En total dos casos que pasan a añadirse a los dos anteriores.

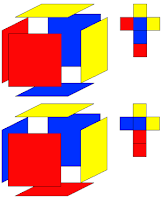
Ninguno opuesto

Si no queremos poner los rojos opuestos entre sí, ni los azules, podemos colocar los rojos en el lateral (uno junto a otro), y los azules, de forma que uno sea opuesto a un rojo y otro a un amarillo. Hay dos formas distintas de hacerlo, pero pueden parecer cuatro, hasta que giremos el cubo cambiando de sitio las caras amarillas y veamos que dos de ellas coinciden con las otras dos. En las imágenes vemos la vista y el desarrollo de las dos formas distintas, con la cara roja en primer plano. Si cambiamos las amarillas de sitio, tendremos las dos formas que no tienen la cara roja en primer plano.

Así, en total hay sólo seis formas distintas de pintar el cubo con estas condiciones.