Triángulos isósceles en un polígono

Enunciado

En este caso, yo empezaría a probar combinaciones concretas. Probablemente, después introduciría un orden entre ellas para asegurarme de citar todos los casos posibles, y no repetir ninguno (o los menos posibles). Y en todos ellos, buscaría los triángulos pedidos. Si además descubro una ley general, mejor (la hay, este problema es un caso particular de uno más genérico propuesto en una fase de la Olimpiada Matemática Española).

Rojos y azules

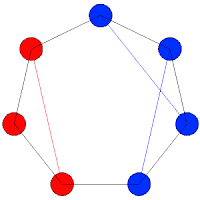
Si dejamos juntas las cuatro no marcadas (de azul), se produce una combinación del tipo oooxxxx, como la que vemos en el dibujo contiguo. Vemos que se pueden formar tres triángulos isósceles, 1-2-3 (rojo), 4-5-6 y 5-6-7 (azul). He numerado los vértices en el sentido de las agujas del reloj, empezando desde el primero rojo.

Segunda opción

Si sólo permitimos tres azules juntas, la otra debe estar entre dos rojas, con lo que se pueden dar dos casos que resultan ser simétricos. Por tanto, quedan reducidos al del dibujo (ooxoxxx), donde también se pueden contar tres triángulos, azules todos ellos, 3-5-7, 3-6-7 y 5-6-7.

Tercera elección

Si hay a lo sumo dos azules juntas, las dos restantes pueden estar juntas o no, por lo que da lugar a dos situaciones claramente distintas, salvo simetrías. Sus esquemas son ooxxoxx y oxoxoxx. La primera de ellas tiene también tres triángulos, que son 1-2-5, 3-4-7 y 3-6-7.

Última situación

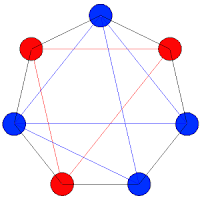
Por otra parte, la otra variante tiene (como no podía ser de otra forma tres triángulos isósceles monocromáticos, 1-3-5, 2-4-6 y 2-4-7.

No puede haber más posibilidades, ya que siempre han de quedar al menos dos azules juntos, puesto que hay más azules que rojos.

Isósceles en un hexágono

¿Y si hubiese seis vértices solamente? El resultado no sería igual. En primer lugar, observamos que en la colocación oooxxx habría dos triángulos (1-2-3 y 4-5-6), mientras que en ooxoxx no habría ninguno. Además, en el caso oxoxox tendríamos el problema de encontrarnos con dos triángulos equiláteros (que podrían ser tratados a todos los efectos como isósceles, pues dos lados iguales también tienen).