Círculos

Enunciado

Líneas útiles

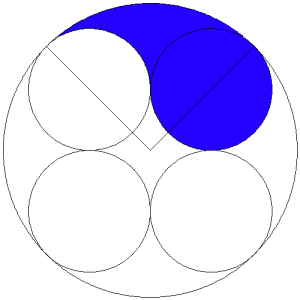
Como de costumbre en los problemas de cálculo de áreas o distancias, estudiaremos los radios de las circunferencias implicadas, de forma que voy a dibujar los dos radios de la circunferencia mayor que atraviesan por el centro a la circunferencia coloreada y a su vecina, como se ve en el dibujo adjunto.

Desplazando fragmentos

Es claro que puedo trasladar la mitad coloreada de la circunferencia que queda debajo del radio a la mitad de la circunferencia sin colorear que queda por encima del otro radio, sin que varíe el área coloreada (ver el segundo dibujo).

Ahora, el área coincidirá casi totalmente con la cuarta parte de la circunferencia grande, a la que tendremos que quitar un pequeño fragmento de área que calcularemos luego.

Calculando medidas

¿Qué radio tiene la circunferencia grande? Si dibujo los radios de las circunferencias pequeñas que se tocan en los puntos tangentes, estoy dibujando un cuadrado. Un radio de la grande que pase por uno de los vértices del cuadrado tiene de longitud media diagonal del cuadrado más el radio de la circunferencia pequeña. Como el lado del cuadrado mide 2 (centímetros), medio diámetro medirá raíz de 2, y el radio de la grande, por tanto, uno más raíz de 2. El área de un cuarto de circunferencia será, por tanto ese radio al cuadrado por pi y dividido por cuatro, es decir, aplicando el cuadrado de la suma, tres más dos por la raíz de dos, todo ello multiplicado por pi y dividido por cuatro.

El centro

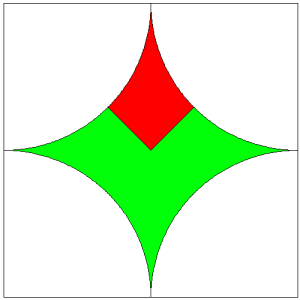
Pero falta calcular el área del pequeño fragmento central, que habrá que restar. Si observamos de cerca el centro del dibujo, veremos que el fragmento que debemos quitar es la cuarta parte del objeto central del dibujo. Visto así, el objeto al completo (sombreado en dos colores en el dibujo) se ve como la diferencia entre un cuadrado y cuatro cuartas partes de un círculo, es decir, un círculo completo. Es decir, que el área del objeto completo sería 4 menos pi, por lo que su cuarta parte sería 1 menos pi cuartos.

Valor final

Por tanto, restar ambos valores sería la solución, cuya expresión sería pi (sumar tres pi cuartos más un cuarto de pi), más raíz de 2 entre 2 por pi, menos uno, lo que da la expresión representada en la imagen. Su valor aproximado es 4,363034123 centímetros cuadrados.