Un cuadrado en cinco rectángulos

Enunciado

Este problema es muy sencillo de plantear. Puesto que sabemos las áreas y los lados, basta que empecemos a asociar los que pueden dar como resultado ese producto.

Lo primero que debemos hacer es confirmar que tenemos área para cubrir los 121 centímetros cuadrados que se nos pide. En efecto, 9 + 16 + 18 + 28 + 50 = 121

Por ejemplo, 9 centímetros cuadrados sólo podría obtenerse multiplicando 3 por 3 o 9 por 1, puesto que los lados son números enteros. Como cada lado mide una cantidad distinta, este rectángulo debe ser de 9 por 1 centímetros.

De forma similar, 16 no puede ser más que 2 por 8.

El cuadrado de área 50 se puede conseguir únicamente multiplicando 5 por 10, porque los dos factores han de estar entre 1 y 10.

También es sencillo 28, que debe ser 4 por 7.

Y los dos lados que sobran, 3 y 6, forman el rectángulo de 18.

Juntamos los dos más largos

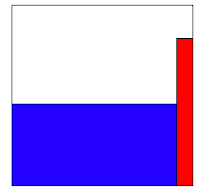
¿Cómo colocar los cuadrados? Empezamos con el de lado 10, que tiene casi la longitud del cuadrado completo. La única forma de completar 11 es que situemos junto a él el rectángulo de lado 1 por 9, como indica la primera figura. Evidentemente, lo podemos girar y desplazar hasta ponerlo en varias posiciones, pero todas son equivalentes.

Tercer rectángulo

Ahora, entre el rectángulo de lado 9 y 11, que es el lado del cuadrado, debemos poner el rectángulo de lado 2 por 8, y esto se puede hacer de dos formas, que en realidad son la misma, vista en un espejo, salvo desplazamientos de la pieza más grande. Se trata de la segunda figura.

Como antes, entre el lado 8 y el resto del cuadrado únicamente podemos poner el rectángulo de tamaño 3 por 6.

Cuadrado completo

Evidentemente, podemos comprobar que el hueco que queda en el centro de estos cuatro rectángulos mide, en área, lo mismo que el rectángulo que nos sobra, como no podía ser de otra forma, por la suma que hicimos antes. Lo más curioso es que realmente también coincidan sus lados, como podemos comprobar, sumando 11 entre todos.