Área descubierta

Enunciado

Dibujo figura

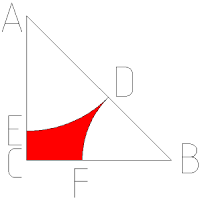
Como podemos apreciar en el dibujo, la figura que buscamos es una figura irregular, delimitada por los segmentos FC y CE, y los arcos de circunferencia ED y DF. Aparentemente, no responde a ninguna fórmula típica para cálculo de área. Como se ha conseguido a partir de eliminar zonas de un triángulo de área conocida, podemos tratar de llegar a averiguar su área mediante restas, siempre que podamos averiguar las áreas que hemos eliminado o cubierto. Hemos de observar que los ángulos en A y B son de 45 grados, es decir, que las zonas delimitadas por los sectores circulares AED y BFD son la octava parte de un círculo completo, cuya área podemos obtener a partir de su radio.

El primer arco trazado, AED, es de área conocida, la mitad del triángulo ABC. Como el área de este triángulo es 2*2/2 = 2 unidades de área, el área de AED será de una de estas unidades. Sin embargo, el otro arco se traza tangente a DE en D, de forma que lo único que sabemos es que su radio completa la hipotenusa del triángulo ABC, AB, uniéndolo al anterior.

Nos hace falta calcular el radio del primer arco, AED, y deducir de él el del otro, BDF, para poder calcular el área que cubre. Como el área de AED es 1 y es la octava parte del círculo completo, ese círculo tendrá área 8, y su radio será la raíz cuadrada del cociente de 8 entre pi.

Fórmula del radio

Puesto que el segmento AB es la hipotenusa de ABC, su longitud será la raíz de 8 unidades. por lo que el radio del otro sector circular, se calculará restando a raíz de 8 el resultado anterior (ver expresión de la imagen).

Ahora, para hallar el área de la circunferencia, es necesario elevar ese radio al cuadrado y multiplicarlo por el número pi, de donde queda, aplicando el cuadrado de la resta, la expresión 8 más 8 por pi menos 16 por la raíz cuadrada de pi. El área del sector será la octava parte, es decir, 1 más pi menos 2 por la raíz cuadrada de pi.

Solución

Ahora queda calcular el área de la zona que buscamos, restando a 2 (área del triángulo) el área del primer sector (1) y el área del segundo (la expresión citada anteriormente), quedando la expresión del resultado como queda en la imagen, 2 por la raíz cuadrada de pi menos pi, que tiene un valor aproximado de 0,403315048.