Puntos alineados

Enunciado

Un cuadrado y dos triángulos equiláteros

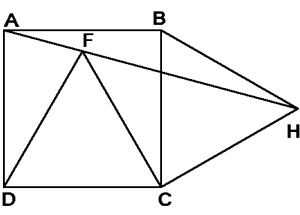
Si empezamos por hacer el dibujo como aparece junto a estas líneas, y unir los puntos que supuestamente están alineados, veremos de forma sencilla que AD, DC, CF y CH son líneas que miden exactamente lo mismo, es decir, que los triángulos ADF, DFC y CFH son isósceles (DFC es. además, equilátero) y sus ángulos son fácilmente medibles.

Para confirmar que AF y AH son segmentos de una misma recta, nos basta con ver que los ángulos AFD, DFC y CFH suman 180 grados.

Como DFC es equilátero, FDC mide 60 grados y ADC 90, por lo que ADF mide 30. Por ser ADF isósceles, DAF y DFA miden 75 cada uno (para poder sumar 180 en total). Es decir, que DFA mide 75 grados.

El ángulo DFC mide claramente 60 grados.

Por simetría con lo ya visto, FCB mide 30, y BCH mide 60 por ser BCH triángulo equilátero. En total, FCH mide 90. Como el triángulo FCH es isósceles, los ángulos CFH y CHF miden ambos 45 grados, de la misma manera que antes. Es decir, que CFH mide 45 grados.

Por lo tanto, AFH mide AFD + DFC + CFH = 75 + 60 + 45 = 180 grados, es decir, que AF y AH están sobre la misma recta, y A, F y H están alineados.