La parcela

Enunciado

Primer paso en la parcela

Varios lectores han dado su solución, y han acertado, pero este problema no debe ser resuelto utilizando ecuaciones, ya que muchos de los participantes en este nivel no las conocen.

El único comentario que, hasta el momento, lo ha resuelto con otro sistema, ha sido el de Lluís Usó, que ha usado el truco de tratar de resolverlo como si fuesen pesos en una balanza (de estos problemas hay muchos), poniendo en cada lado piscinas, casas o jardines como le interesaba manteniendo el equilibrio. El resultado me ha parecido tremendamente original.

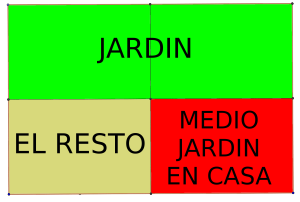
Otra manera de verlo es geométrica, explotando poco a poco la información que nos dan. En el primer dibujo podemos ver representado en una parcela rectangular, el jardín por un lado y por otro el espacio que ocupan casa y piscina, que dicen ser iguales.

Segundo paso de la división

En segundo lugar, nos fijamos en que la casa es igual a medio jardín y una piscina, de forma que hemos dibujado medio jardín dentro de la casa, y hemos dejado sin rellenar el espacio que ocupan el resto de la casa y la piscina.

Y por último, viene la fase más delicada, que es el momento en que nos damos cuenta que en ese espacio sin delimitar caben exactamente dos piscinas, la de verdad, y la que cabe dentro de la casa junto con el medio jardín.

División final de la parcela

En este dibujo podemos apreciar claramente las proporciones entre casa, jardín y piscina, de forma gráfica. Así, observamos que la piscina ocupa la mitad de medio jardín, es decir, que el jardín ocupa lo que cuatro piscinas, y que la casa ocupa lo que tres piscinas. Y como la piscina se nos dice en el problema que mide 30 metros cuadrados, resulta que la casa ocupa 90, el jardín 120, y la parcela en su totalidad 240 metros cuadrados.

Otra forma de abordarlo puede ser tantear los diferentes valores para ver si cumplen las igualdades, no al azar, si no de manera inteligente hasta forzar todas las condiciones. Éste método lo han seguido algunos de los que participaron en la fase. Podemos ver algunas respuestas siguiendo este enlace.