Equivalencia entre propiedades
Construcción de una semicircunferencia
En el enunciado encontraréis dos demostraciones muy claras, una basada en producto vectorial y geometría analítica una y la otra en propiedades elementales como el teorema de Tales y los ángulos internos de un paralelogramo.
Quería dar una visión diferente, basada en una combinación de Teorema de Tales y el ángulo inscrito.
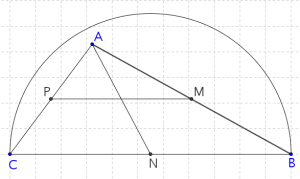
Trazamos una semicircunferencia centrada en N y de radio CN (o NB, puesto que son iguales). Observa que cualquiera de estas distancias es, debido al teorema de tales, igual a PM, ya que P y M son los puntos medios de los lados AC y AB, por lo que PM mide la mitad que CB.
De esta forma, el ángulo CAB es obtusángulo si A está dentro del semicírculo que hemos dibujado, por el principio del ángulo inscrito, y eso es equivalente a que AN es más corta como distancia a PM = CN = NB.
Si A está exactamente sobre la circunferencia, AN será igual a PM, y eso equivale a que el ángulo CAB sea recto.
Por último, si el punto está fuera de la circunferencia, lo que equivale a que el segmento AN sea mayor que PM (recuerda que es igual a CN y a NB), eso es totalmente equivalente a que el ángulo CAB sea agudo.
No hay comentarios:
Publicar un comentario