Un punto del tetraedro

Enunciado

Tetraedro regular

Tetraedro desplegado

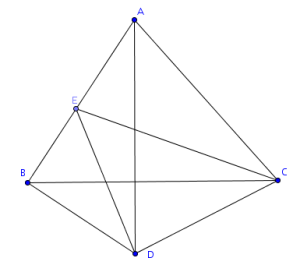
He preparado dos vistas del tetraedro, para que se vea en perspectiva y desplegado, que suelen ser las mejores formas de abordar un problema tridimensional.

Aquí se aprecia que el ángulo CED está en un triángulo isósceles, esté donde esté el punto E dentro de la arista. Esto es debido a la simetría de la figura, ya que los segmentos ED y EC están dentro de dos triángulos equiláteros iguales, y son simétricos respecto al eje AB.

Debido a esto, el ángulo CED será mayor cuando la longitud de ambos segmentos sea lo menor posible (por ejemplo, aplicando el teorema de los senos, o el del coseno, por ejemplo, pero también mediante trigonometría elemental, aplicada a los triángulos rectángulos que se obtienen al cortar en dos triángulos rectángulos un triángulo isósceles).

Evidentemente, la longitud mínima de estos segmentos se obtiene cuando el segmento ED (y el EC) es perpendicular al segmento AB, y en ese caso E está exactamente en el centro, debido a que tanto ACB como ADB son triángulos equiláteros.

Así que el valor máximo se da cuando el punto es el punto medio.