Cuando coinciden tres ángulos

Enunciado

Dibujo las líneas

En el dibujo podemos ver un triángulo genérico en el que se han dibujado las líneas que se usan en el dibujo. Como podemos ver, las tres líneas no tienen que coincidir necesariamente en un punto en un triángulo cualquiera, ni tienen que ser iguales los ángulos.

Sin embargo, la igualdad que plantea el problema (CAL, ABH y BCM iguales como ángulos) no se cumple en todos los casos. Veamos en qué situaciones se verifica y qué debe cumplir el triángulo ABC.

El ángulo CAL, igual que el ABH, es la mitad que BAC, por ser AL bisectriz de BAC. Por otra parte, AHB es un ángulo recto, por ser BH una altura de AC. Si nos fijamos en el triángulo AHB, se trata de un triángulo rectángulo y sus dos ángulos agudos deben sumar uno recto, siendo uno el doble del otro. Está claro entonces que BAC es un ángulo de 60 grados y ABH, de 30.

Inmediatamente nos viene a la cabeza un triángulo célebre, el equilátero. En este, coinciden bisectriz, altura y mediana, por lo que se cumple la igualdad de ángulos. La pregunta que queda por responder es ¿habrá algún otro tipo de triángulo que lo cumpla?

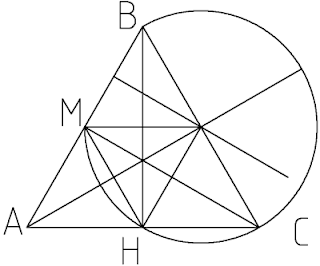
Si existe tal tipo de triángulo, ABH coincidirá con la mitad de un equilátero, y podremos marcar M, que es el punto medio del lado AB. El punto C estará sin duda sobre la recta AH, y al unirlo con B y M formará un ángulo de 30 grados, como el que forma el vértice del equilátero.

Otra solución

Como en otros problemas, tenemos un segmento y buscamos un punto que al unirlo forme el mismo ángulo que uno que tenemos, por lo que debemos trazar un arco que pase por esos tres puntos, como aparece en el dibujo. Si hay un segundo punto de corte entre el arco y la recta AH, ese es otro posible punto. En el dibujo, parece que coincida con el punto H, pero eso ya lo aclararemos más adelante. Indudablemente este punto formará otro triángulo que cumplirá la condición que se pide.

El centro del arco

Si trazamos las mediatrices de los vértices del triángulo BMC, resulta evidente que el centro del arco que pasa por los tres puntos es el centro del lado BC (del triángulo equilátero), por lo que pasará por H, y por tanto el triángulo ABH cumple también la condición, y es el único que lo hace además del triángulo equilátero. Es decir, que o los ángulos del triángulo inicial son todos iguales, o bien son 60 en A, 30 en B y 90 en C.