Simetrías en un triángulo

Enunciado

Puntos simétricos y triángulo

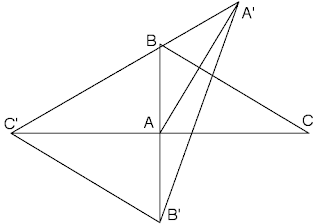
Si dibujamos la situación que se nos pide en el ejercicio, y añadimos las líneas perpendiculares a los lados que llevan de cada vértice a su simétrico, veremos pronto que (si el triángulo inicial es rectángulo en A), ABC y AB'C' son, realmente, el mismo triángulo girado.

Mi primera intención para estudiar el área fué dividir el triángulo en zonas y estudiarlas por separado. Evidentemente, ésta zona tenía la misma área que el triángulo original, pero fui incapaz de encontrar nada interesante del resto del triángulo A'B'C'.

Completando la altura

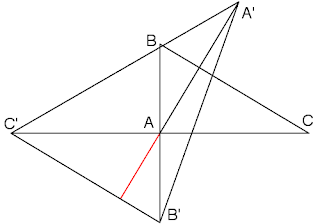
Sin embargo, cuando traté de calcular el área de este triángulo, me llevé una sorpresa. No puedo conocer fácilmente a partir del primer triángulo los lados B'A' y A'C', pero sí el B'C'. Además, al dibujar su altura, me llevé una gran sorpresa. Observa (línea en rojo) que está alineada con la altura del triángulo original, que coincide con la mitad de la línea entre A y A'. Por supuesto, eso quiere decir que la altura del triángulo A'B'C' es el triple que la altura del triángulo ABC, teniendo ambos la misma longitud de base. Evidentemente, esto significa que el área de A'B'C' es triple que la de ABC.

Al parecer, para que se dé esa igualdad, es necesario que el triángulo sea rectángulo. Si usas en su lugar un equilátero, por ejemplo, el área del triángulo generado es cuatro veces mayor que el original, como es fácil de apreciar.