Construir un triángulo equilátero

Enunciado

Triángulo equilátero

Imaginemos que tenemos el triángulo ya construido. Dos puntos caen sobre la circunferencia (y a partir de esos dos puntos, evidentemente, podemos tener el triángulo completo, pues tenemos la medida del lado). Si unimos el centro con ellos dos, obtenemos un triángulo isósceles, que siempre se puede dividir en dos triángulos rectángulos iguales, trazando la altura desde el centro. Claro, que esta altura es altura también del triángulo equilátero, que por su simetría coincide con la bisectriz, la mediana y la mediatriz.

Como pasa por A (el punto externo), observamos que divide al triángulo en dos triángulos rectángulos, cuyo ángulo agudo (en A) es de 30 grados, la mitad de un ángulo de un triángulo equilátero. Y esa recta, recuerda, pasa por A y por el centro (O) de la circunferencia. A partir de aquí, construimos el método, como detalla Lluís en sus comentarios.

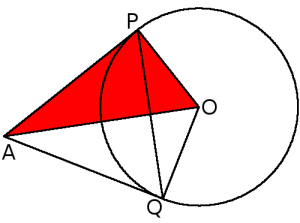
Dados el punto y la circunferencia, unimos el punto (A) con el centro de la misma (O). Levantamos sobre esta recta un triángulo equilátero (da igual su tamaño), uno de cuyos vértices es A. Trazamos su bisectriz en A, de forma que tenemos una recta que forma 15 grados con AO. Esta recta puede intersecar o no con la circunferencia, pero si lo hace, levantamos una perpendicular a AO que pase por uno de estos puntos de intersección (P), que cortará a la circunferencia en otro punto (Q). El triángulo APQ es un triángulo equilátero.

Evidentemente, en muchos casos intersecará en dos puntos distintos, con lo que, como mucho, podemos construir dos triángulos equiláteros distintos que cumplan estas condiciones. Puede ser que sólo tengamos uno, en cuyo caso, el lado del triángulo será tangente a la circunferencia.

Triángulo equilátero máximo

Si el punto estuviese algo más alejado, la recta no cortaría a la circunferencia, con lo que no existiría este tipo de triángulo. El caso límite es, claramente, el tangente, en cuyo caso se forma un triángulo rectángulo de 30 grados (en rojo en el dibujo) en el que el radio (recuerda que mide 1) es uno de los catetos. Por eso, la hipotenusa mide 2, y el punto A está a 2 unidades del centro de la circunferencia, o, lo que es lo mismo, a una única unidad de la circunferencia.