Otro problema de policubos

Enunciado

La primera misión, descubrir los 8 policubos de orden 4, ya ha sido abordada muchas veces en este blog. Por ejemplo, en la solución anterior, Más dados pegados. Copio aquí esa parte para tener presentes los nombres de los policubos que usaremos.

Para descubrir las ocho figuras, la forma más metódica consiste en partir de las figuras que se forman con tres cubos (dibujo del enunciado) y unirle uno más de todas las formas posibles, evitando repeticiones.

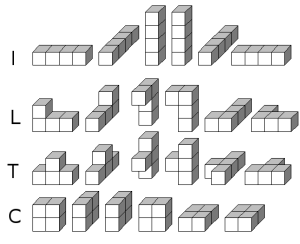
En los dibujos he dibujado seis veces cada figura, para que se vean frontalmente las seis vistas que ofrece.

Cuatro policubos de orden 4

Así, en efecto, partiendo de la tira de tres cubos, obtenemos la tira de cuatro cubos (I), la l (L), y la T (T). Todos los otros puntos donde añadimos un dado se pueden situar de una de estas tres formas. Partiendo de la l de tres cubos (la otra figura), podemos obtener otras cinco figuras nuevas, el simétrico cuadrado (C), un ortoedro 2x2x1, la s que recuerda a dos de las piezas del tetris (S), y tres que no son planos, pues surgen de añadir un dado hacia "fuera" del plano formado por la l de tres dados. Podemos llamar a uno esquina (E), si el dado añadido es en el centro de la l, y a los otros dos izquierdo (Z) y derecho (D), pues, aunque no son iguales, al situarlos rente a un espejo, uno sería igual al reflejo del otro (se dice que son imágen especular uno del otro).

Otros cuatro policubos

Una vez descubiertas y clasificadas las ocho formas, vamos a poner de manifiesto las relaciones entre ellas y las de orden 3, como pide nuestro segundo reto.

Es fácil descubrir la I de orden 3 en los policubos I, L y T, por lo que estos tres contienen la I de orden 3.

Todos los policubos de orden 4, excepto la I, contienen la L de orden 3, es decir, que la L y la T contienen ambos policubos de orden 3.

El tercer reto es el más complicado, y aquí me temo que Lluís se equivoca, o no he entendido bien su descripción. Pensemos que un policubo de orden 7 que contenga a todos los de orden 4 debe contener a la I y a la C. Evidentemente, estos dos conjuntos de cubos deben tener algo en común, ya que si no sumarían 8 cubos.

Si sólo tuviesen un cubo en común, cada uno de los 7 cubos de la figura pertenecerían a uno o a otro. Como contienen a la S, que debe tener al menos 3 cubos en común con la C, la I debe estar en el mismo plano que la C, por lo que toda la figura estaría en el mismo plano, y no podría contener a E, Z o D.

Doce policubos de orden 7

Luego deben tener dos cubos en común, porque no pueden tener más de dos en común. Dada la simetría de las dos figuras estarán dispuestas de forma que, o bien C está centrada, o bien está en un extremo.

Y la figura tiene un cubo que no está en el mismo plano. Ese cubo debe tener una cara en contacto con la C, ya que en caso contrario no podría contener alguno de los policubos E, Z o D. Por tanto, si quitamos las posibilidades que se pueden girar y coincidir con otra, sólo hay 12 figuras distintas posibles, que aparecen reflejadas aquí. Es sencillo, aunque laborioso, ver que todas ellas contienen los 8 policubos de orden 4.