Más dados pegados

Enunciado

De nuevo Lluís ha dado en el clavo en sus comentarios.

Para descubrir las ocho figuras, la forma más metódica consiste en partir de las figuras que se forman con tres dados (dibujo del enunciado) y unirle uno más de todas las formas posibles, evitando repeticiones.

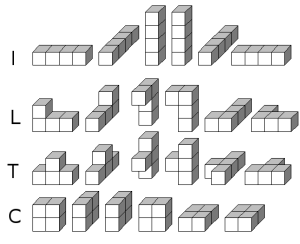
En los dibujos he dibujado seis veces cada figura, para que se vean frontalmente las seis vistas que ofrece.

Cuatro policubos de orden 4

Así, en efecto, partiendo de la tira de tres cubos, obtenemos la tira de cuatro cubos (I), la l (L), y la T (T). Todos los otros puntos donde añadimos un dado se pueden situar de una de estas tres formas. Partiendo de la l de tres cubos (la otra figura), podemos obtener otras cinco figuras nuevas, el simétrico cuadrado (C), un ortoedro 2x2x1, la s que recuerda a dos de las piezas del tetris (S), y tres que no son planos, pues surgen de añadir un dado hacia "fuera" del plano formado por la l de tres dados. Podemos llamar a uno esquina (E), si el dado añadido es en el centro de la l, y a los otros dos izquierdo (Z) y derecho (D), pues, aunque no son iguales, al situarlos rente a un espejo, uno sería igual al reflejo del otro (se dice que son imágen especular uno del otro).

Otros cuatro policubos

Ahora que conocemos las ocho figuras bien, vamos a calcular cuántos puntos podemos lograr que aparezcan en su superficie. Si has estudiado el ejemplo que hemos propuesto (con tres dados), los puntos que usamos son todos los que pueden aparecer en la superficie de la figura, es decir, todos los puntos de todos los dados excepto los que están tapados por estar en la cara en la que se unen dos dados. Lo ideal sería que aprovecháramos estas caras para ocultar la mayor cantidad de puntos posibles, y eso es precisamente lo que intentaremos. Cada dado tiene en su exterior 21 puntos, sencillamente trataremos de ver cuántos puntos tapamos, y los descontaremos del total, que serían 21*4 = 84.

En el caso de la I, en los dos dados de los extremos podemos tapar el 6, pero en los dos centrales sólo podremos tapar en total 7 (y da igual cómo los pongamos), así que en total quedan 84 - (6 + 6 + 7 + 7) = 58 como mínimo en el exterior.

En el caso de la L, en los extremos de nuevo tapamos 6, en el que hace esquina, podemos tapar el 6 y el 5, pero en el otro sólo podemos tapar un total de 7, en total tapamos 6 + 6 + 7 + 11 = 30, de forma que en el exterior quedan 54 puntos como mínimo.

La T tiene tres dados que sólo tienen una cara tapada, que podemos hacer que sea la del 6, pero el dado central tiene dos caras opuestas, que suman 7 independientemente de cómo las situemos, y otra más, que podemos hacer que sea también el 6. En total, tapamos como mucho 6 + 6 + 6 + 13 = 31, así que podemos reducir los puntos exteriores a 53.

La figura C es excepcional, pues sus cuatro dados no tienen tapadas caras opuestas, así que en todas podemos tapar el 5 y el 6, de forma que podemos llegar a tapar 11*4 = 44 puntos, quedando tan sólo 40 en el exterior.

La S tiene un estudio sencillo: las dos puntas pueden estar tapando el 6, y los centrales se pueden situar para que tapen el 6 y el 5, así que como 6*2 + 11*2 = 34, el exterior tiene como mínimo 50 puntos.

La E tiene tres puntas (un 6 tapado, a lo sumo), y la central tiene tapadas tres caras no opuestas, así que pueden ser 6, 5 y 4. La suma total sería 6*3 + 15 = 33, y la puntuación mínima exterior sería de 51 puntos.

La Z y la D son simétricos, de forma que su estudio es similar. Las puntas se pueden tapar 6, y las otras dos un 6 y un 5, pues no tapan caras opuestas, de forma que pueden tener en el exterior 50 puntos como mínimo, al igual que la S.