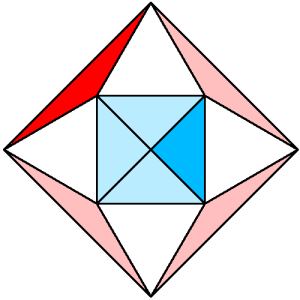
Dos triángulos distintos

Enunciado

Triángulos y cuadrados

Lo primero que hemos de hacer en este tipo de problemas es realizar el dibujo con la máxima precisión posible. En el caso del que acompaña estas líneas, hemos dibujado todos los triángulos de tipo 1 y de tipo 2 posibles sobre un cuadrado, para dibujar una figura simétrica. Eso puede dar una idea bastante aproximada de cómo llegar a calcular las áreas de esas figuras. En nuestro caso, hemos pintado de rojo uno de los de tipo 1 (y de rosa los demás), y de azul uno de los de tipo 2 (y de azul claro los demás).

Una de las formas más directas de calcular el área de un triángulo es buscar una base medible, y una altura que no sea difícil de calcular, usando simetrías o el teorema de pitágoras.

En nuestro caso, hay un sistema más directo, ya que entre cuatro de los de tipo 2 forman el cuadrado inicial, por lo que sabemos que su área es la cuarta parte. Si el lado del cuadrado fuese 2 unidades, por ejemplo, su área sería 4 unidades cuadradas, y el área de un triángulo de tipo 2 sería 1 unidad cuadrada.

De la misma forma, podemos tratar de alcanzar las dimensiones del triángulo de tipo 1 mediante medición de bases y alturas, pero también podemos ver todo el cuadrado donde están dibujados todos los elementos, y ver los triángulos de tipo 1 como la diferencia entre el área total y la suma de los triángulos equiláteros y el cuadrado central.

En cualquier caso, parece que necesitamos el lado de ese cuadrado grande, pero en realidad no es así. Se puede calcular (y alguno de nuestros alumnos lo hizo), pero aquí voy a trabajar sin calcularlo.

Suponiendo que el lado del pequeño es 2, la altura del triángulo equilátero de lado 2 divide a éste en dos triángulos rectángulos iguales, uno de cuyos cateto mide 1 y la hipotenusa, 2. Es evidente que esa altura mide la raíz cuadrada de 3 (√3), por el Teorema de Pitágoras. Y, claro, la mitad de la diagonal del cuadrado grande es esta altura más la mitad del lado del cuadrado, es decir, 1 + √3. Dos medias diagonales forman un cuadrado de tipo 2, pero del triángulo grande, es decir, que el área del cuadrado grande será 4(1 + √3)(1 + √3)/2 = 2(1 + √3)(1 + √3) = 2(1 + 2√3 + 3) = 8 + 4√3.

Ahora bien, el área de uno de los triángulos equiláteros será 2√3/2 = √3, por lo que el área de los cuatro triángulos será 4√3, y el área del cuadrado será 4, por lo que la diferencia entre el cuadrado grande, los triángulos equiláteros y el cuadrado pequeño, será de 4 unidades cuadradas. Es decir, que el área de cada triángulo de tipo 1 será de 1 unidad cuadrada, que es igual a la del tipo 1.

Si, son exactamente iguales.