Coincidencia de centros

Enunciado

Este problema incluye dos conceptos que debemos revisar previamente para buscar la solución: el centro de la circunferencia inscrita (incentro) de un triángulo y el centro de la circunferencia circunscrita (circuncentro) de otro triángulo. ambos triángulos tienen dos puntos en común (B y C), y uno de los ángulos es la mitad de otro, pero eso lo consideraremos más adelante.

Incentro

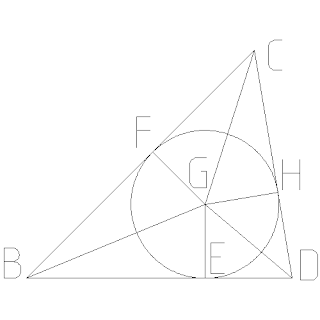
Empecemos por el incentro. Su principal característica es que es el centro de la circunferencia inscrita, por lo que ésta es tangente a los tres lados. De ahí, las verticales de los lados al centro (en el dibujo, GF, GE y GH) miden todas lo mismo (el radio de la circunferencia). Por otra parte, para que el incentro esté a la misma distancia de los tres lados, pertenece a las tres bisectrices interiores de los mismos, de forma que las líneas que lo unen a los vértices del triángulo (en el dibujo, GB, GC y GD) dividen en dos ángulos iguales a cada uno de los vértices. La coincidencia de ángulos y longitudes hace que, en cualquier incentro, se den unas curiosas igualdades de triángulos rectángulos, que en el dibujo serían CFG = CGH, BEG = BFG y DEG = DEH. Y esto llevaría a unas consideraciones sobre áreas que no nos interesan ahora.

Circuncentro

Vamos con el circuncentro. Su principal característica es que está a la misma distancia de los tres vértices del triángulo, por lo que los segmentos que lo unen a los tres vértices (en el dibujo, GA, GB y GC) son de la misma longitud, por lo que los triángulos que se forman con dos de esos segmentos (en el dibujo, BCG, BAG y ACG) son isósceles. Para estar a la misma distancia de dos puntos, se debe estar sobre la perpendicular por el centro (mediatriz) al segmento que los une. Por eso se suele calcular el circuncentro intersecando las perpendiculares a los lados por su centro. Dicho de otra forma, las perpendiculares desde el circuncentro a los lados del triángulo (en el dibujo, GE, GF y GI) lo dividen en dos segmentos iguales. También esta circunstancia daría lugar a más consideraciones, pero nos vamos a conformar con esta información, de momento.

Los dos centros

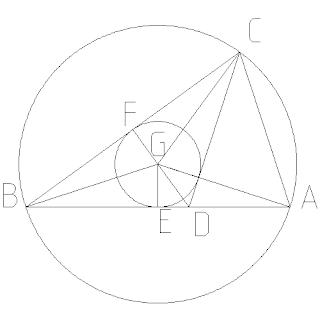
Vamos ya a nuestro problema. Representamos la información que nos dan, trazando los radios más significativos de las dos circunferencias concéntricas (tienen el mismo centro), y vamos a observar algunas propiedades del dibujo. Por ser circuncentro, G divide el ángulo DCB en dos iguales, que serán la cuarta parte de ACB, ya que CD divide en dos partes iguales a este ángulo.

Por otra parte, por ser G circuncentro, CF = BF, por lo que el triángulo BFG es idéntico a CFG, así el ángulo CBG es el mismo que GCB. Este ángulo parece importante, vamos a ponerle un nombre, llamémosle x. Esto significa que ACB mide 4x. Pero GB es bisectriz de ABC, por lo que ABG también mide x, así que ABC mide 2x.

Vamos a tratar de llegar al último de los ángulos del triángulo inicial. De nuevo E parte en dos segmentos iguales a AB, por ser G circuncentro, de donde AEG es igual a BEG, y de nuevo el ángulo x aparece en BAG. Y como CG y AG son radios de la circunferencia circunscrita, ACG es isósceles en G, por lo que el ángulo CAG es el mismo que ACG, 3x. En definitiva, CAB es de nuevo el ángulo 3x + x = 4x.

Como en todos los triángulos, sus ángulos deben sumar 180 grados, en este caso 4x + 2x + 4x = 10x, de donde x mide 18 grados.

Por esta razón, los ángulos del triángulo ABC son 72 en A y en C, y 36 en B. Esto me ha permitido dibujar con precisión el dibujo, ya que en los borradores que hice a mano no se "apreciaba" tan claramente la coincidencia de centros.