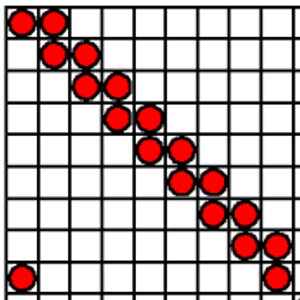
Monedas en un tablero

Enunciado

Las que están en la diagonal a partir de la novena fila y la novena columna, sólo se pueden elegir si se selecciona una fila o columna en la que estén, así que es necesario utilizar siete de las filas o columnas (da igual) de las que disponemos para quitar estas siete monedas.

Zona tablero

Por esto, el problema queda reducido a quitar, seleccionando nueve filas o columnas (pero no más de 8 del mismo tipo) en el cuadrado 9x9 donde están las 18 restantes.

Observamos que debemos quitar dos en cada una de las selecciones, ya que no hay fila o columna que tenga más de 2 monedas, y 9*2 = 18.

Si quitamos la moneda que está separada quitando las de su fila, dejaremos una moneda solitaria en la última columna, por lo que la única manera de seleccionarla será quitando la fila en la que se encuentra, la octava. Esto dejará una moneda suelta en la octava columna (séptima fila), y obligará a retirar la fila 7. De la misma manera, tendremos que retirar todas las filas hasta la primera, con lo que necesitamos usar nueve filas, en lugar de las 8 que nos permite el problema, por lo que no es posible hacerlo así.

Si quitamos la moneda separada quitando la columna, razonamos del mismo modo, y deberíamos seleccionar nueve columnas, cosa que tampoco es posible.

Luego, efectivamente, no es posible quitar esas 25 monedas con las condiciones que se nos ha dado.