Primer problema de la Iberoamericana 2008

Enunciado

Evidentemente, es una barbaridad empezar a trabajar con un tablero de 2008 por 2008 casillas. Empecemos con uno más manejable de 4 por 4. ¿Por qué 4? Trabajar con 2 no tiene mucho aliciente, y con 3, al ser un número impar, aparece una "molesta" casilla central, que no sale en el original y que tal vez "estropee" el razonamiento. Dicho esto, advierto que yo empecé pensando en uno de 3 por 3, y como no llegué a nada concreto, pasé a 4.

Muestra de tablero 4x4

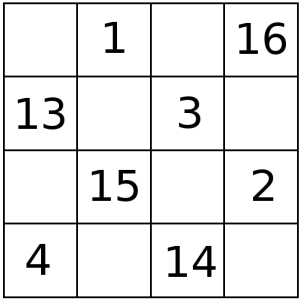
Disponemos de 16 números. En cada fila (y columna) restaremos el mayor del menor, y buscamos obtener la cifra mayor posible. Lo primero que se me ocurrió es poner al 16 y al 1 en la misma fila (primera), y al 2 en la misma columna que el 16. Si ponemos el 15 en la misma fila que el 2, y la columna del 1, tendremos dos filas y dos columnas que darán el máximo posible (15, 14, 14, 13). No importa lo que pongamos en las casillas de esa fila y esa columna, así que busquemos las que faltan y nos encontramos que son 4, en dos filas y dos columnas. Las mayores diferencias que puedo lograr son de 12 con 3 y con 4, y de 11 con esos dos números. No importa cómo distribuya los demás, las mayores diferencias serán 15, 14, 14, 13, 9, 8, 8, 7. La suma total de esas diferencias será de 14*4 + 8*4 (ya que 15 + 13 = 14*2, y 9 + 7 = 8*2) , que nos da 88.

¿Estamos seguros de que es el máximo valor posible? Podemos razonar que, si en algún momento nos desviamos de este método, sacamos valores menores, sin poder aumentar los demás. Por ejemplo, si ponemos el 15 en otra fila o columna, no obtendremos el 14 o el 13, obtendremos números menores, y en la otra fila como mucho los aumentaremos en la misma cuantía que disminuyamos ésta. Es decir, que puede que haya tras distribuciones que den el mismo resultado, pero no que lo mejoren.

De la misma forma, podemos generalizar el método para nuestra tabla de lado 2008. Para captar más el sistema de trabajo, pensemos en cómo sería en un tablero de 6 por 6. 36, 35, 1 y 2 estarían combinados en dos filas y dos columnas para proporcionar 35, 34, 34 y 33. Por su parte, 34, 33, 3 y 4 se usarían para dar 31, 30, 30 y 29, y por último 32, 31, 5 y 6 darían 27, 26, 26 y 25. La suma total sería (34 + 30 + 26)*4 = 90*4 = 360.

En el caso que nos ocupa, como 2008² = 4032064, las primeras (y mayores) diferencias serían 4032063, 4032062, 4032062 y 4032061, que tienen de promedio 4032062, e irían bajando de 4 en cuatro a lo largo de 1003 pasos hasta la última, que tendría de promedio 4032062 - 1003*4 = 4028050. Cada uno de esos promedios, en la suma, iría multiplicado por cuatro. Al sumar los 1004 sumandos, como las diferencias de uno al siguiente son constantes, podríamos agrupar el primero con el último, el segundo con el penúltimo, y así sucesivamente, para conseguir que todas las parejas sumasen igual, que sería 4032062 + 4028050 = 8060112, número que se sumaría un total de 1004 veces y se multiplicaría por 4, es decir, que el valor máximo buscado sería 8060112*1004*4 = 32369409792 exactamente.