Distancias en circunferencias tangentes

Enunciado

Desde luego, este problema es el más difícil de todos los de la fase local de este año, al menos para mi gusto. Ninguno de los métodos directos que he probado han dado fruto, y sólo una construcción bastante artificiosa resuelve el problema. No veo ningún método que permita abordarlo de manera más directa, y agradecería a alguien que lo conozca que lo cite en los comentarios.

Lo primero que se me ocurrió, y que era imprescindible para abordar el problema, era transformar el producto en un cociente, de forma que nos permita tratar con semejanzas.

Circunferencias tangentes

En efecto, es equivalente |PN'|⋅|MN| = |PN|⋅|M'N'| a la igualdad |PN'|/|M'N'| = |PN|/|MN|, donde ambos cocientes representan una proporción de los lados de un par de triángulos, PNM y PN'M'.

En segundo lugar, conviene trazar varios ejemplos en versión grane del dibujo correspondiente y comprobar que las igualdades se cumplen. Para trazar el dibujo, unimos dos puntos al azar del plano, que acabarán siendo los centros, y elegimos un punto en el segmento que los une, que será el punto de tangencia. Usando ambos puntos, y las distancias al punto entre ambos, trazamos las circunferencias. Escogemos el candidato a punto A, (no conviene que sea demasiado simétrico respecto al dibujo), y trazamos las tangentes (lo unimos al centro opuesto con un segmento, y levantamos una circunferencia del que sea diámetro. Los puntos de corte serán los puntos de tangencia M y M', borrando las líneas auxiliares después). Si medimos los segmentos que necesitamos para la igualdad, comprobaremos que es cierta.

Usar varios puntos A sobre la misma circunferencia nos puede aportar una pista que es fundamental para resolver este problema. Si usamos el mismo par de circunferencias, el cociente que calculamos ¡no depende de la posición de A! Esta observación nos será muy útil para enfocar el problema a calcular uno de los cocientes con independencia de A, con lo que el problema quedará resuelto. Cualquier cociente de ese tipo que se construya con una tangente a la circunferencia, dará el mismo resultado.

Buscando ángulo igual

Mi primera intención era tratar de comprobar una semejanza entre ambos triángulos, pero queda descartada por el primer ejemplo que dibujo. Después, el intento de calcular algún cociente partiendo de la posición de A, usando los radios de las circunferencias para construir triángulos rectángulos resulta infructuoso, de forma que trato de reducir al mínimo el número de líneas buscando alguna relación que facilite el acceso a este cociente. Es entonces cuando vuelvo a la observación de la que hablo en el párrafo anterior, centrándome en el dibujo segundo. Basta, por tanto, calcular |PN|/|MN| independientemente de A.

Hay un resultado sobre arco capaz que es muy conveniente conocer para realizar este problema: la recta tangente a un extremo de la cuerda forma con ésta un ángulo igual al del arco capaz.

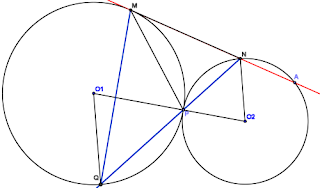
Si reconocemos en el dibujo esta situación, veremos que el ángulo PMN coincide en esta posición, de forma que será igual al ángulo de cualquier ángulo inscrito en el arco que define MP. Esto nos permite situar un ángulo idéntico, dentro de la circunferencia C₁, usando cualquier punto. Aparentemente esto no nos sirve para establecer ninguna relación, hasta que nos demos cuenta de que, si prolongamos el segmento PN, obtenemos un punto Q muy interesante. Como ya sabemos, MQP (y MQN) forma el mismo ángulo que PMN, y QNM es el mismo ángulo que PNM, con lo que tenemos una semejanza da triángulos entre PNM y QNM, que da la clave para la resolución del problema.

Sin embargo, esto no nos permite aún calcular ese cociente de forma sencilla.

Proporción definitiva

Transformamos el cociente |PN|/|MN| en |MN|/|QN| por la semejanza calculada. Parece que no hayamos avanzado, pero disponemos de una herramienta fundamental, ya que el punto P pasa por el semento QN, formando dos nuevos triángulos O₁PQ y O₂PN con los radios de las circunferencias, es decir, que se trata de dos triángulos isósceles, que tienen un ángulo en común (en realidad dos, pues es el que está repetido) y son semejantes. Por tanto, si llamamos r₁ y r₂ a los dos radios, tenemos que |PQ|/r₁ = |PN|/r₂, con lo que |QN| = |QP| + |PN| = |PN|r₁/r₂ + |PN|, es decir, |QN| = |PN|(1 + r₁/r₂). En realidad esta proporción se puede observar a simple vista, debido a la semejanza de ambas circunferencias y los arcos que define esta recta.

De esta situación, tenemos que |PN|/|MN| = |MN|/|QN| = |MN|/(|PN|(1 + r₁/r₂)) = (|MN|/|PN|)*(1/(1 + r₁/r₂)). Pero |PN|/|MN| y |MN|/|PN| son inversos uno del otro, por lo que (|PN|/|MN|)² = 1/(1 + r₁/r₂), que no depende de la posición de la tangente, si no del producto de los radios de las circunferencias. Por tanto, el cociente buscado no depende más que de ese producto de los radios de la circunferencia y se cumple así la propiedad pedida.