Partiendo el reloj

Rectas que se cortan

Rectas que no se cortan

Enunciado

Como ya anticipa Lluís en los comentarios, la clave de este problema es ver en cuántos trozos pueden dos rectas dividir al reloj.

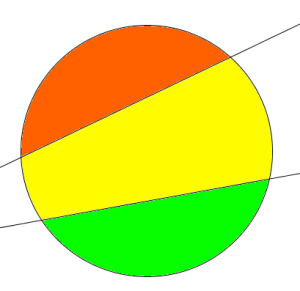
He puesto aquí dos imágenes de ejemplo para que entendáis cómo dos rectas, según que se corten o no, dividen en tres o cuatro partes a la circunferencia.

Una vez que eso se ha estudiado, hay que sumar los números del reloj, lo que resulta 1 + 2 + 3 + ... + 12 = 78, que es divisible entre 3 pero no entre 4. De aquí se deduce que las dos rectas no se deben cortar, y que cada parte debe sumar exactamente 78/3 = 26.

Al menos una de las partes debe tener los números consecutivos, así que debemos estudiar qué números entre 1 y 12 pueden sumar 26 con los números inmediatamente consecutivos.

Con 1 no funciona, pues salta del 21 al 28. Tampoco 2, que va del 20 al 27, ni 3, del 25 al 33. Si empezamos por 4, podemos conseguir el 22 o el 30, pero ninguno intermedio.

Empezando por el 5, conseguimos 26 con el 6, 7 y 8.

Es fácil comprobar que tampoco se consigue nada empezando con 6, 7, 8 , 9 o 10, y con 11 sólo podemos conseguir 21.

Reloj partido

Por tanto, una de las secciones separa los números de 5 a 8 en una zona. Ahora, los restantes números los debemos dividir de forma que ambos grupos sumen lo mismo (26), empezando por 4 o por 9, por ejemplo. Así, si separamos sólo el 4, con los posteriores a 9 hemos de sumar 22 y no podemos. Si usamos 4 + 3 = 7, tenemos que sumar 19 con números a partir del 9, y usaremos, claro está, el 9 y el 10. No hay más maneras de conseguirlo, ya que 4 + 3 + 2 = 9 y 4 + 3 + 2 + 1 = 10, ninguno de los cuales sirve, y aunque usáramos los números anteriores a 1 (12, 11, ...) tampoco conseguimos 26 (10 + 12 = 26, 10 + 12 + 11 = 35).

Entonces está claro que lo dividiremos con líneas que pasan una de ellas entre el 2 y el 3 y entre el 11 y el 10, que dejan una parte del reloj donde están 11 + 12 + 1 + 2 = 26, y la otra entre el 4 y el 5 y entre el 8 y el 9, de forma que en una sección están 3 + 4 + 9 + 10 = 26 y en la otra 5 + 6 + 7 + 8 = 26.