Cuadriláteros circunscritos

Enunciado

Como comenta nuestro anónimo colaborador, este enunciado es relativamente conocido como Teorema de Pitot, y su demostración puede encontrarse fácilmente en Internet si se realiza una búsqueda por este nombre.

Cuadrilátero circunscrito

Pero, planteado como ejercicio, podemos enfrentarnos a él como un problema de geometría, y realizar un dibujo como el que acompaña a estas líneas para razonar sobre él.

En realidad, el cuadrilátero con la circunferencia inscrita puede verse como un conjunto formado por una circunferencia y ocho tangentes (que casualmente están alineadas dos a dos), que parten de cuatro puntos externos a la circunferencia.

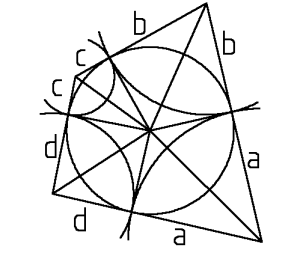
Estudiando la simetría de las tangentes, podemos concluir fácilmente que las longitudes de los pares de tangentes que parten de un mismo punto son idénticas, y nombrar las diferentes longitudes con cuatro letras, por ejemplo, a, b, c y d.

Evidentemente, la longitud de cada lado del triángulo original, en ese caso, está formada por la suma de dos de estas cantidades, pero si se suman las longitudes de un lado con la de su opuesto, descubriremos que en cualquier caso el resultado es a + b + c + d, sean cuales sean los lados escogidos. Por tanto, la suma de las longitudes de dos lados opestos es idéntica a la de los otros dos, como queríamos demostrar.