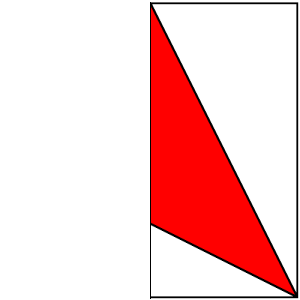
Punta de flecha

Enunciado

Básicamente hay dos enfoques para calcular este área. Uno, que me parece el más sencillo, es ver esta figura como un triángulo grande (cuya base sería la base del cuadrado, y la altura, la altura del cuadrado) al que se le ha quitado un triángulo más pequeño, cuya base sería también la base del cuadrado, pero cuya altura deberíamos calcular.

Flecha dividida

La otra forma se verla, sería cortar el cuadrado verticalmente por la mitad (eje de simetría), de forma que se viese la punta de flecha como dos triángulos, cuya base debemos determinar, y cuya altura es la mitad del cuadrado original.

En cualquier caso, hace falta calcular a qué altura se sitúa el vértice superior del triángulo blanco inferior (M en la descripción del dibujo). Este punto resulta estar a una cuarta parte del total del lado original, es decir, a 0,5 unidades (el lado del cuadrado original es 2, para que su área sea 4). Eso se debe a que el ángulo que forma con la horizontal es igual que el que divide en dos el lado del cuadrado, y se deduce por semejanza.

Una vez conocido este dato, por el primer método obtenemos que el área de la flecha es 2*2/2 - 2*0,5/2 = 2 - 0,5 = 1,5 unidades cuadradas (3/2 de unidad cuadrada).

Del segundo método, obtendríamos que el área de cada triángulo es (3/2)*1/2 = 3/4, por lo que la flecha tendría de área 2*3/4 = 3/2 de unidad cuadrada.